[Time-series 논문 리뷰] Time series data augmentation classifier for industrial process imbalanced fault diagnosis

0. Abstract

• 산업 고장 진단에서 고장 분류는 일반적인 문제임
  • classifier는 대체로 다양한 클래스 간에 동등한 양의 데이터를 가정하에 구축됨
  • 하지만, 산업 공정에서 수집되는 정상과 고장 데이터의 양은 불균형이 대부분임
  ⇒ 문제점의 본질: 고장 분류가 불균형 데이터 분류 문제임
• 문제 해결 방법: 데이터 증강 방법 (더 많은 데이터 생성 & 데이터 균형 맞추는 데에 사용)
  • 생성된 데이터의 품질이 분류 성능에 큰 영향
  ⇒ 생성된 데이터의 품질 보장 위해, 이 논문에선 시계열 데이터 생성의 변이형 오토인코더 사용(VAE)
• 제안하는 것 : 생성된 시계열 데이터 활용하여 불균형 고장 분류 문제 해결을 위한 TSDAC(시계열 데이터 증강 분류기)
  • 테네시 이스트만(TE) 벤치마크 공정에 적용
  • TSDAC는 불균형 고장 분류 문제에 적합한 방법

---

1. Introduction

• (데이터 처리 관점) 분류 알고리즘을 개선하여 불균형 데이터 문제를 해결하는 다양한 방법이 개발
  • K-means Bayes 알고리즘
  • 불균형 데이터를 가진 비선형 다중 분류 문제를 다루기 위해 K-means 기반 SVM-tree 알고리즘
  → 한계점: 이러한 방법들은 데이터를 기반으로 한 특수한 설계를 요구하며 다른 데이터로 확장하기 어려움
  • 오버 샘플링, 언더 샘플링 방법을 통해 데이터를 삭제하거나 채워서 데이터를 균형있게
    • 오버 샘플링 방법은 데이터를 보충함으로써 데이터의 양을 균형있게 함.
    → 한계점: 보충된 정보가 좋은 것인지 나쁜 것인지 판단하기 어렵고, 이는 모델에 불확실성을 가져옴. 데이터의 복잡성이 증가함에 따라, 오버 샘플링 방법을 사용하여 실제 데이터를 모방하기는 더 어려워짐.
    • 언더 샘플링 방법은 일부 데이터를 제거하여 데이터 균형있게 함.
    → 한계점: 삭제된 데이터의 정보는 모델 구축에 사용될 수 없으며, 이 역시 분류 성능이 떨어지게 할 수 있습니다.
  ⇒ 따라서, 불균형 데이터 문제를 해결하기 위해 생성 모델이 개발됨.
• 생성 모델의 발달로 산업 불균형 데이터에 대해 연구됨
  • deep feature generation network
  • VAE
    • 무작위 언더샘플링과 조건부 VAE
    • TimeVAE: 다변량 시계열 생성 위함
  • GAN
    • 불균형 대용량 데이터 증강 및 고장 분류를 위해 가우스 판별 분석을 돕는 GAN
• 데이터 증강 분류기(DAC) (이 논문이 영감 받은 것)
  • 분류 과정
  • GAN사용하여 데이터 생성 → 생성된 데이터의 무작위성 고려하여, 생성된 데이터를 필터링하기 위한 데이터 선택 전략 제안 (데이터 선택하여, DAC는 데이터 균형 달성) → 지도학습 방법과 결합하여, 불균형 고장 분류
  • MDAC (다중 불균형 고장 문제 해결위함)
    • 동적 시계열 데이터 처리 불가
  ⇒ 따라서, 드문 고장 데이터 생성하고 불균형 고장 분류 방법 개발해야됨 !
• Contribution: TSDAC (Time Series Data Augmentation Classifier)
  • 1) 불균형 고장 데이터가 있는 동적 공정 다룰 수 있음
  • 2) 정지된 공정의 경우, TSDAC는 데이터 연속화&재사용하여 데이터 생성의 안정성 향상 가능
  • 3) 시계열 데이터 양을 균형잡고, 분류 성능 향상 가능

---

2. Preliminaries

2.1. VAE

 

2.2 Time variational autoencoder (TimeVAE)

 

---

3. Time series data augmentation classifier (TSDAC)

3.1. Step1) Serialize the process data

• 비연속 데이터(non-dynamic processes and non-time series data)일때 사용하여, 데이터의 양 확대& 드문 데이터 정보 강화 가능 (이미 시계열 데이터일때는 필요X, 바로 3.2 수행ㄱ)

• 예시 Fig3
  • 6개의 샘플을 포함하는 데이터 세트는 직렬화할 길이를 선택함으로써 다른 시리즈 데이터로 변환될 수 있음. 만약 시퀀스 길이(t)를 2로 선택한다면, 원본 데이터 세트는 5개의 시계열 샘플을 포함하는 데이터 세트로 변환됨.

⇒ 따라서 이 방식으로 비연속 데이터 처리하면, 데이터 세트는 선택된 시계열 길이에 따라 다양해짐. 시퀀스의 길이는 데이터 수집의 빈도와 공정의 반응 시간을 종합적으로 판단해야 됨.

 

3.2. Step2) Time series data generation

TimeVAE는 time series 데이터 생성을 위해 사용됨.

• 인코더
  • TimeVAE의 인코더는 기본 VAE와 유사함.
• 디코더
  • 디코더는 재구성을 생성하기 위한 시간적 구조를 가지고 있음.
  • 디코더에서, $N$은 배치 크기, $D$는 잠재 변수의 수, $T$는 시간 단계의 수를 나타냄.
  • 이 시간적 구조는 추세 블록, 계절 블록, 잔차 블록으로 구성됨.

3.3. Step3) Data augmentation classifier

• 원본 불균형 시계열 데이터(TS)+ 생성된 시계열 데이터 = 균형 잡힌 증강 데이터

• Fig 6해석
  • MLP와 softmax를 사용하는 시계열 데이터 증강 분류기(TSDAC)를 설계

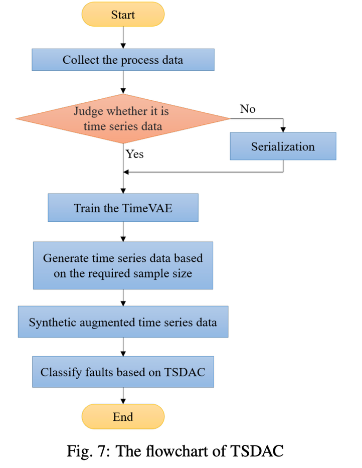
• Fig 7 해석
  • 증강된 시계열 데이터는 원본 문제를 균형 잡힌 시계열 데이터 분류 문제로 변환할 수 있음.
  • t가 1과 같을 때 TSDAC는 DAC로 저하된다는 점을 언급할 필요가 있습니다.

---

4. Case study

 

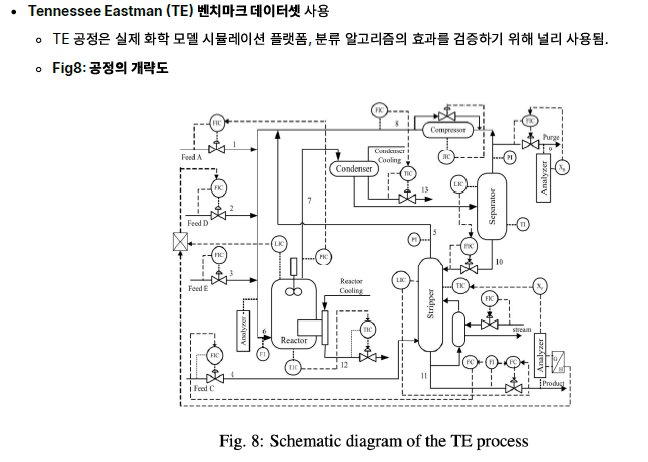
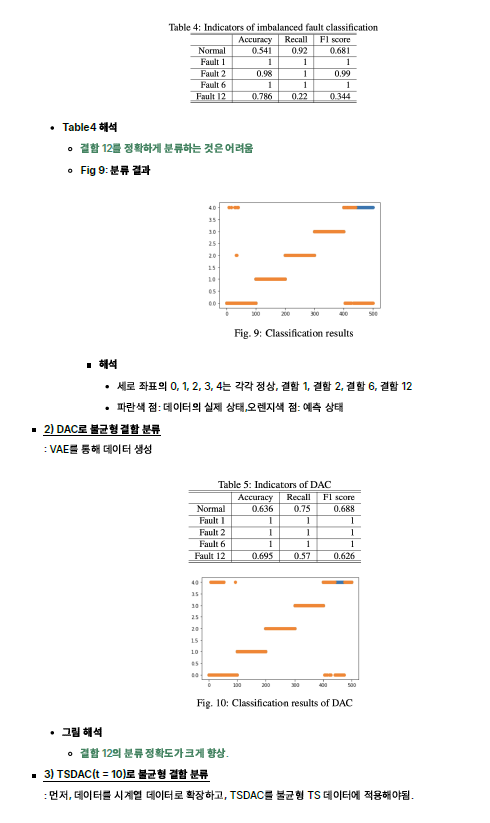
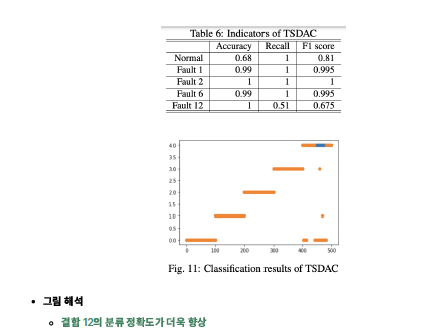
• 결과 요약
  • 불균형 데이터를 직접 분류하는 것은 분류 성능이 떨어지는 결과를 초래. (1번째 상황)
  • 생성된 데이터가 증강 데이터를 형성하는 경우에도 마찬가지. (2번째 상황)
  • 그러나 생성된 데이터를 사용하여 데이터셋을 증강하면 더 나은 분류 결과를 얻을 수 있음. (3번째 상황)
    • 즉, TSDAC는 불균형 결함 데이터에 대해 최고의 분류 성능을 달성 가능함.
  • (= 데이터를 시계열로 확장하고 이를 증강시키면 성능을 더욱 향상시킬 수 있음.)