0. Abstract
- 제안된 접근법
- 제한된 샘플 수에서 핵심정보 추출&진단&예측 솔루션 개발
- 고장 진단관련해서, 3개의 실제 데이터셋+2가지 유형의 기계학습 방법 사용
1. INTRODUCTION
- 문제 상황 정의
- 데이터 부족 문제: PHM(장비 및 시스템의 고장 진단 및 예측) 라벨이 없거나, 사용 가능한 경우에도 신뢰할 수 없는 경우
- → 성능 떨어지거나 실행가능하지 않을 수 있음.
- 해결법: 데이터 증강 방법으로 해결하는 연구 많이 수행됨
- 제안하는 모델(TVAR)
- 시간 변화하는 자기회귀(TVAR)모델 기반으로 다변량 시계열 데이터 증강을 위한 방법
- 목표: 부족한 데이터에서 정보 추출 & 진단 및 예측 솔루션의 품질개선할 수 있는 방식으로 추가 샘플 생성 & 비정상 시계열 직접 처리 가능
2. BACKGROUND ELEMENTS
2.1. Considerations About The Time Series Data
- 제안하는 모델로 증강될 시계열 데이터셋에 대한 가정
- A1) 동일 데이터셋의 시계열은 동일하게 샘플링됨
- A2) 동일 클래스의 시계열은 동일 다변량, 잠재적으로 비정상적인 확률 과정으로 모델링
- 잠재적 비정상 행동: 확률 과정의 attribute가 시간에 따라 변화할 수 있음
⇒ 제안된 데이터증강은 A2)로부터 파생됨.
(주어진 클래스의 시계열을 모델링하기에 적합한 확률과정 찾는 것, 그것으로 새로운 시계열 생성)
2.2. Considerations About The Time Series Models
- TVAR
- 매개변수가 시간이 지남에 따라 변할 수 있게함 → 데이터 비정상성 더 잘 포착
- **기저함수(가중치 및 모델 차수의 집합)**에 의해 제어됨.
- 예시1년 동안 한 도시의 온도를 추적한다고 상상해 보세요. 온도는 시계열 데이터입니다. 일년 내내 계절에 따라 온도가 변합니다. 여름에는 더 따뜻하고 겨울에는 더 춥습니다. 시간에 따른 온도 특성의 이러한 변화는 비정상성의 예입니다.TVAR 모델을 입력하세요. TVAR 모델에서는 매개변수가 시간이 지남에 따라 변경될 수 있습니다. 이는 모델이 계절 변화에 따라 동작을 조정할 수 있음을 의미합니다. 여름 동안 모델은 기온이 더 높은 것이 더 일반적이라는 것을 학습하고 이에 따라 예측을 조정할 수 있습니다. 겨울에는 기온이 낮아지는 추세를 인식하고 적응합니다.따라서 온도 예를 사용하면 TVAR 모델은 온도의 계절적 변화를 설명하기 위해 매개변수를 조정하고 시계열 모델에 대한 동적 및 적응형 접근 방식을 제공함으로써 일년 내내 더 정확한 온도 예측을 허용합니다.
- 매개변수를 변경하는 TVAR 모델의 기능은 일련의 가중치와 모델 차수를 포함하는 TVAR 기본 기능에 의해 제어됩니다. 가중치는 미래 기온을 예측하는 데 있어서 과거 기온의 중요성을 결정하고, 모델 순서는 모델이 예측을 하기 위해 얼마나 오래 전으로 보이는지 결정합니다.
- 전통적인 자기회귀(AR) 모델에서는 매개변수(이전 온도가 미래 온도 예측에 어떻게 영향을 미치는지 결정)가 일정하게 유지됩니다. 이 모델은 짧고 안정적인 기간 동안에는 잘 작동할 수 있지만 변화하는 계절에 적응할 수 없기 때문에 일년 내내 어려움을 겪습니다.
- TVAR(Time-Varying Autoregressive) 모델은 특히 시간이 지남에 따라 데이터 특성이 변하는 비정상성(non-stationarity)으로 알려진 시계열 데이터 모델링을 위한 강력한 도구입니다. 이해하기 쉬운 예를 들어 이를 단순화해 보겠습니다.
- 동일 클래스에 속하는 시계열이 동일한 TVAR 표현을 공유할 것 (A2가정에 의해)
- 예시'정상 작동' 클래스에 속하는 로봇의 센서 데이터는, 로봇이 제대로 작동할 때의 진동 및 온도 패턴을 반영합니다. 예를 들어, 정상 작동하는 로봇은 일정한 진동 수준과 온도 범위를 유지할 수 있습니다. TVAR 모델을 사용하여 이 클래스의 시계열 데이터를 모델링하면, 정상 작동 상태에서의 일반적인 진동 및 온도 변화 패턴을 포착하고 예측할 수 있습니다.이렇게 하면, 각 클래스에 속하는 로봇의 센서 데이터에서 공통적으로 나타나는 패턴이나 추세를 효과적으로 모델링할 수 있으며, 이를 통해 로봇의 작동 상태를 정확하게 모니터링하고 필요한 유지보수를 예측할 수 있게 됩니다. 이는 제조 공장에서의 생산성과 효율성을 높이는 데 큰 도움이 될 수 있습니다.
- 반면에, '비정상 작동' 클래스에 속하는 로봇의 센서 데이터는, 로봇에 문제가 있을 때 나타나는 이상 진동이나 온도 변화를 반영합니다. 예를 들어, 부품 마모나 고장으로 인해 진동 수준이 갑자기 증가하거나 온도가 비정상적으로 변할 수 있습니다. 동일한 TVAR 모델을 이 클래스에도 적용하면, 비정상 작동 상태에서의 진동 및 온도 이상을 식별하고 모델링할 수 있습니다.
- 예를 들어, 제조 공장에 여러 대의 조립 로봇이 있고, 각 로봇에서 진동 센서와 온도 센서를 통해 데이터를 수집한다고 가정해봅시다. 이 데이터는 시간에 따라 변화하는 여러 변수들로 구성된 시계열 데이터입니다. 이제 이 로봇들을 '정상 작동'과 '비정상 작동'의 두 클래스로 분류한다고 합시다.
- (= 정상/이상 각 클래스 별로 공통적으로 나타나는 패턴이나 추세 포착)
- 매개변수가 시간이 지남에 따라 변할 수 있게함 → 데이터 비정상성 더 잘 포착
2.3. TVAR Model
3. DATA AUGMENTATION WITH TVAR
3.1. Overview of the Proposed Method
- TVAR 모델을 사용하여 주어진 클래스에 속하는 시계열의 기본 확률 과정을 표현(A2 참조).
- 이러한 확률 과정은 데이터로부터 계산된 경험적 통계에 의해 설명될 수 있다고 가정.
- TVAR 모델에 적합한다는 것은 TVAR 과정의 일차 및 이차 표현식이 데이터에 대해 계산된 경험적 통계와 일치하도록 하는 매개변수와 보간 함수를 찾는 것을 의미합니다.
- 적합한 TVAR 매개변수와 보간 함수를 찾은 후, 이를 TVAR 과정 공식(식 7 참조)에 다시 대입
3.2. TVAR Sub-Models for the Mean and Covariance

3.3. Interpolation Functions and Empirical Statistic
3.3.1. Computing the Empirical Statistic

3.3.2. Finding the Interpolation Function (시계열 데이터 분석을 위한 보간 방법)

3.3.3. Sinusoidal Regression


4. EXPERIMENTAL STUDY
- 세팅
- 2가지 ML모델 아키텍처 & 3개의 공개 센서 시계열 데이터셋
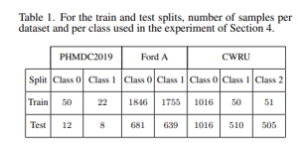
4.1. Datasets
4.2. Machine Learning Models
- 세부 사항
- 선택한 RF 아키텍처는 50개의 추정기와 최대 깊이 5를 가지고 있습니다.
- Python 패키지인 tsfresh (Christ, Braun, Neuffer, & Kempa-Liehr, 2018)를 통해 추출.
4.3. Data-Augmentation Procedures
- 목표: 이 연구의 목표는 제안된 증강 방법의 분류 성능과 경쟁 접근 방식 성능 비교
- (TSAug) 경쟁 접근 방식: TSAug (Arundo Analytics, 2023)에 의해 제공되며, 시계열 데이터를 위한 일련의 일반적인 증강 변환을 제공
- 선택된 변환
- i) 표준 편차의 ±10% 변동 범위 내에서 시계열에 흰색 가우시안 노이즈 (WGN) 추가.
- ii) 데이터 포인트의 10%를 무작위로 삭제하고 0으로 채움.
- iii) 무작위로 위아래로 이동하는 데이터 포인트 시리즈 생성.
- iv) 일부 데이터 포인트의 시간 해상도 (샘플링)를 줄임. iii) 및 iv)의 경우 최대 다섯 개의 데이터 포인트 시퀀스를 고려.
- 변환 시뮬레이션
- 센서 데이터의 일괄 처리 시 자주 발생하는 무작위 변동 및 아티팩트를 시뮬레이션
- TSAug 라이브러리는 입력 시계열에 대해 변환 i)에서 iv)를 무작위로 적용하여 새로운 합성 시계열을 생성
- (TvarAug) 제안된 증강 방법:
- P = 4, 6, 8, 10, 12, 14에 대해 계산.
- 각 보간된 곡선에 대해 표 2의 매개 변수 값을 고려하여 TVARm 및 TVARc 표현이 생성됨.
- TVAR 표현의 잡음은 WGN(0,1) 프로세스로 설정됨.
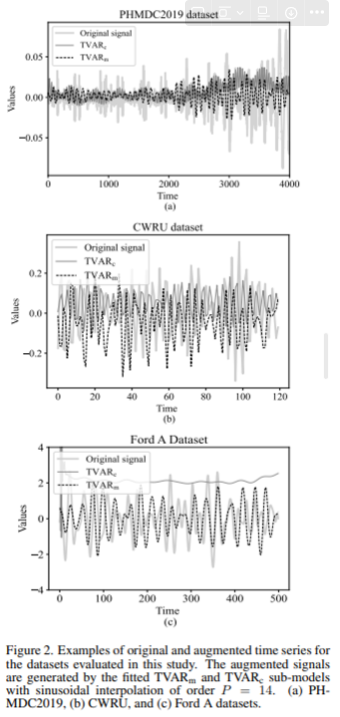
- 예시와 시각화
- TVARm 및 TVARc 하위 모델의 매개 변수 값을 사용하여 얻은 증강된 시계열의 예시가 Fig2에 표시됨.
- 결과
- 전반적으로, 증강된 데이터는 새로운 합성 신호 세그먼트를 생성하기 위해 필요한 확률적 수준을 도입하면서 원래 시계열의 동적 패턴을 잘 캡처
4.4. Test Results
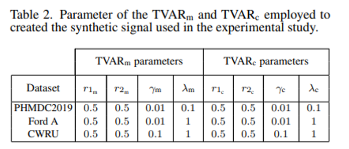
- Table 2
- 걍 파라미터 전부 같은 세팅으로 한 것
- TVARaug와 TVARaug_sub 모델의 매개변수
- γ1과 γ2는 각각 모델들의 매개변수로, 다양한 데이터셋(PHMCD2019, Ford A, CWRU)에 적용
- Table 3
- RF(Random Forest)와 CNN(Convolutional Neural Network) 모델들의 정확도 비교
- "NoAug"는 데이터 증강이 적용되지 않은 기준 결과
- "TSaug"와 "TVarAug"는 각각 시계열 데이터 증강 기법이 적용된 결과
- 해석
- CWRU 데이터셋에 대해 RF 모델을 사용했을 때 증강 기법이 높은 정확도 향상을 보여줌
- TVARaug 방식은 평균적으로 높은 정확도를 보여주며, 특히 어려운 데이터셋에서 성능이 더 우수함