📌 본 내용은 Michigan University의 'Deep Learning for Computer Vision' 강의를 듣고 개인적으로 필기한 내용입니다. 내용에 오류나 피드백이 있으면 말씀해주시면 감사히 반영하겠습니다. (Stanford의 cs231n과 내용이 거의 유사하니 참고하시면 도움 되실 것 같습니다)📌
(📁 아래에 똑같이 제가 정리해놓은 블로그 참고..! 벨로그에 있는게 더 상세히 정리 잘 되어있습니다)
https://velog.io/@ha_yoonji99/Michigan-DLcs231n-10%EA%B0%95-Training-Neural-Networks-Part1
[Michigan DL/cs231n] 10강: Training Neural Networks (Part1)
🔥Michigan University Deep Learning 10강🔥
velog.io
1. Activation Functions : Sigmoid
📍 3가지 문제점: saturated gradient, not zero-centered, 연산비용
- 전체 흐름
-
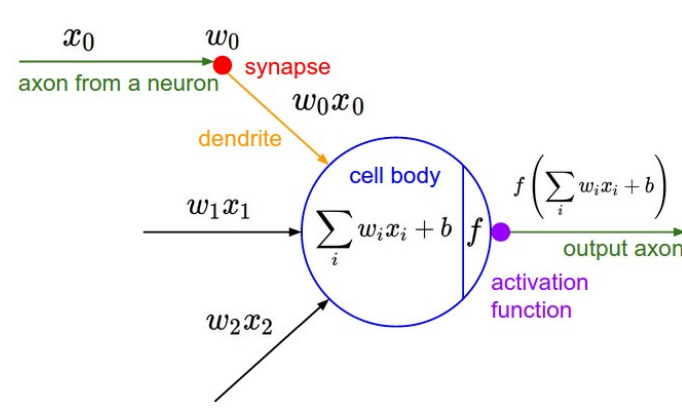
1) 소개

- 개념
- 가장 classic 함
- 존재 or 부재에 대한 확률적 해석
- 0~1사이로 만듦
- “Firing rate” of neuron
- 다른 들어오는 뉴런으로부터 신호 받은 후, 일정 속도로 신호 발화
- 모든 입력의 총 속도에 비선형성 의존
- ⇒ sigmoid: 발화속도에 대한 비선형 의존성을 모델링 한 것
- 문제점 3가지
a. (젤 문제)포화된(Saturated) 뉴런들이 gradient를 죽임 (= 네트워크 훈련 어렵게 만듦) -
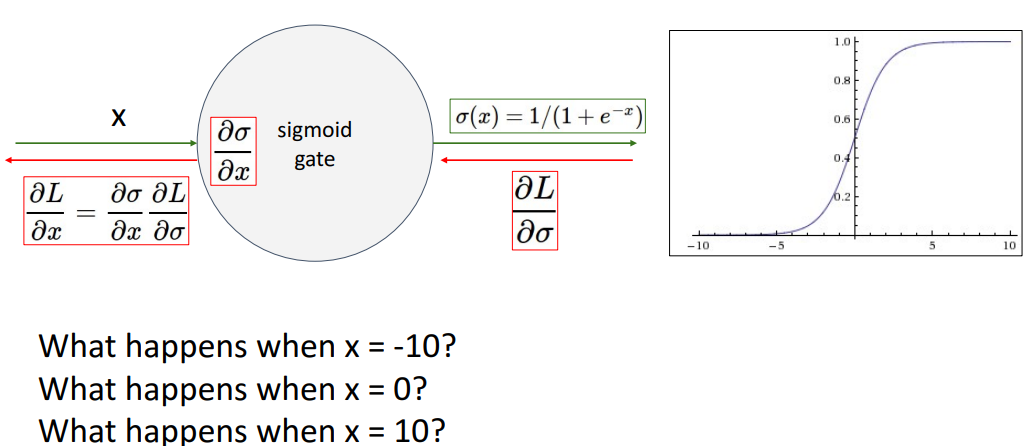
b. sigmoid output들은 zero-centered가 아님
c. 지수함수의 계산비용이 비쌈
2. Activation Functions : Tanh
📍 문제점: saturated gradient

- 개념
- Scaled & Shifted version of Sigmoid
- [-1,1] 범위
- zero-centered함
- 여전히 saturated할때 gradient가 죽음
- saturating non-linearity를 neural network에 사용해야된다면, tanh>sigmoid 사용하는게 합리적
- 그래도 saturated 문제때매 엄청 좋은 선택X
3. Activation Functions : ReLU, Leaky ReLU
📍 문제점: not zero-centered, -일때 gradient vanishing
1) relu
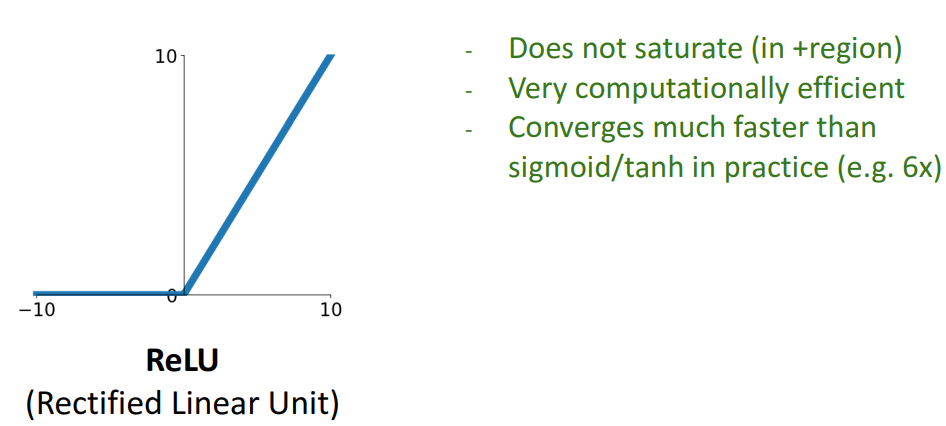
- 개념
- + 영역에서 saturate되지 않음 (=기울기 소실X, killing gradient X)
- 연산 비용 효율적 (cheapest 비선형함수)
- cf) binary와 같이 구현가능, 간단한 임계값만 고려해서 계산비용↓
- sigmoid, tanh보다 매우 빨리 수렴
- cf) 5000 layer같이 매우 깊은 layer면, sigmoid로 수렴하기 매우 힘들것 (batch norm 안쓸때)
- 문제점
- Not zero-centered output (sigmoid와 동일문제)
- relu는 음수X, 모두 + or 0임
- 이런 문제가 있긴하지만 gradient vanishing처럼 심각한 문제는 아니라 괜찮음
- 음수일때의 기울기 문제
-
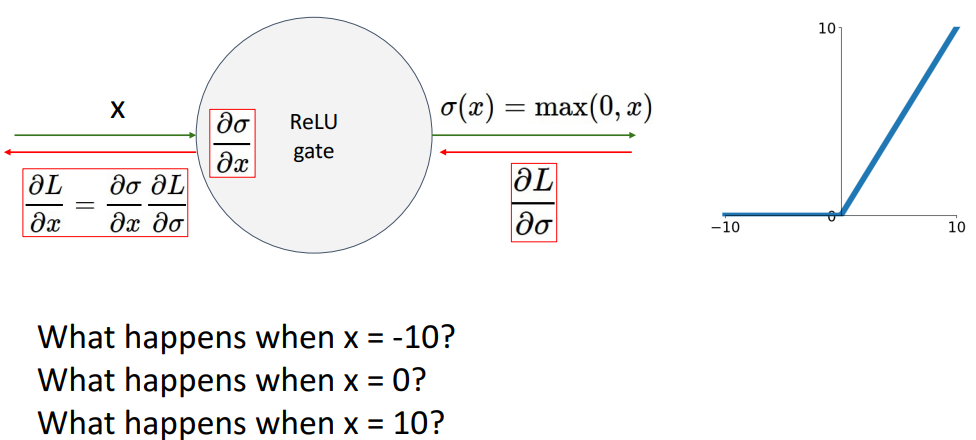
- Not zero-centered output (sigmoid와 동일문제)
2) Leaky relu

- 개념
- 음수일때 작은 + 를 포함함
- 0.01 → hyperparameter임 (각자의 network에 맞게 학습 필요)
- 장점
- saturate되지 않음
- 효율적 연산 비용
- sigmoid, tanh보다 훨씬 빠른 수렴속도
- gradient vanishing되지 않음 ( local gradient가 0이 될 일이 없어서; 음, 양 모두에서)
3) PReLU

- 개념
- leaky relu에서 이어진 것
- $\alpha$ 를 학습해서 알맞게 가져옴 (learnable parameter)
- 스스로 학습 파라미터를 갖고 있는 비선형 함수
- backprop into \alpha
- $\alpha$에 backprop해서 $\alpha$에 대한 손실 도함수 계산 후, $\alpha$에 대한 gradient decent step 만들기
- 문제점) 0에서 미분 불가능 → 해결) 두 방향 중 한 쪽을 고르기 (자주발생X여서 신경안써도됨)
4) ELU (Exponential Linear Unit)

- 개념
- relu보다 더 부드럽고, zero-centered 경향 ↑
- 수식
- $\alpha(exp(x)-1)$ (if x≤0)
- (default $\alpha$=1)
- zero-gradient 피하기 위함
- 약간 sigmoid 모양
- $\alpha(exp(x)-1)$ (if x≤0)
- 문제점
- 여전히 지수함수 포함
- $\alpha$ 때매 학습해야됨
5) SELU (Scaled Exponential Linear Unit)

- 개념
- Scaled version of ELU
- batch norm 제외하고, 깊은 SELU 네트워크 학습 가능
- 장점
- deep neural network + SELU = self normalizing property
= layer가 깊어질수록 → 자기 정규화 속성 ↑
= 활성화 함수 잘 작동 ↑ & 유한한 값으로 수렴
= batch norm과 같은 정규화 제외 가능
- deep neural network + SELU = self normalizing property
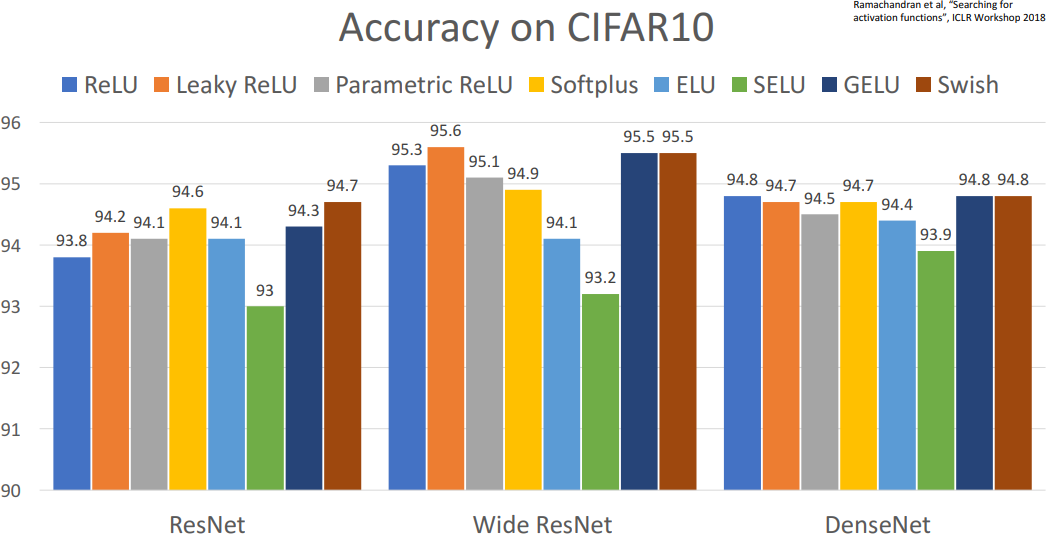
4. Activation Functions : 전체 비교
- 걍 relu써라

5. Data Preprocessing
1) 개념
- 더 효율적 training 위해
2) 방법 2가지
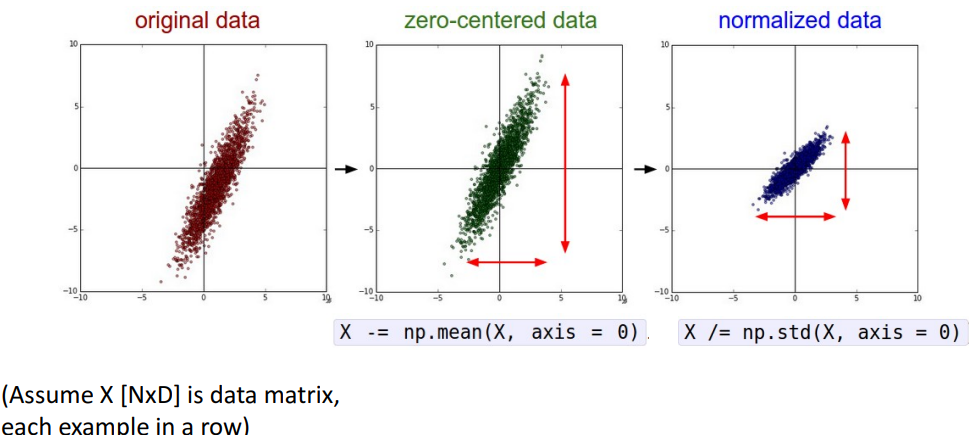
(image data인 경우)
a. zero-center : 평균을 빼서 원점으로 가져옴
- 이렇게 해야 하는 이유?
- 이전에 sigmoid의 문제점으로 gradient가 항상 + or -면, W update도 항상 + or - 되는 문제 지님
- 비슷하게, 여기서도 train data가 모두 + or - 면, W update도 모두 항상 + or -.
- ⇒ 제한적으로 update될 수 밖에 없음*
b. normalized : 동일 분산 갖도록 크기 scaling (표준편차로 나눠서)
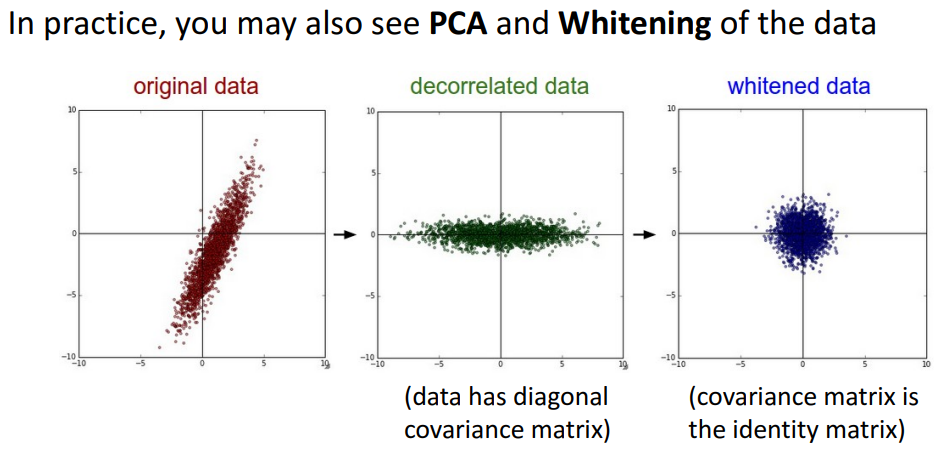
(input이 저차원, 이미지 아닌 경우)
- 원점 중심으로 옮기고 → rotate함
- decorrelated data
- 공분산 matrix ?
- whitened data
- identity matrix
- normalize 전, 후 비교
-
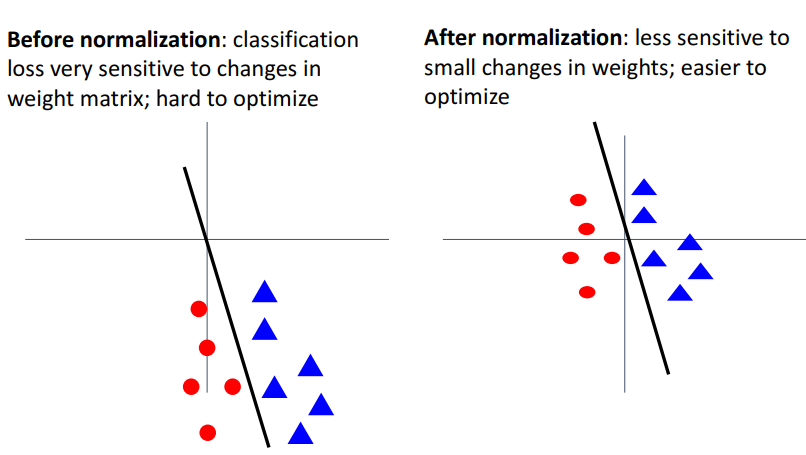
- *(before norm)* **원점으로부터 멀면, weight matrix의 작은 변화에도 큰 변화 발생**→ *optimization process 어렵게 만듦*
- ex. -2x+1 일때 zero-centered 되지 않으면, 함수가 -2.1x+1로 바뀔때, 데이터 분류 상황이 많이 바뀜 → classification loss 많이 변화 → optimization process 어렵게 만듦
- *(after norm)* zero-centered 되어있어서, **W의 작은 변화에 덜 민감**3) 관련 질문들
- Q1. 이런 전처리를 train, test에 적용?
A1. 항상 train에 적용, test에서는 같은 정규화 사용 - Q2. batch-norm사용시에도 전처리 필요?
A2. batch norm을 모든 처리 이전 맨 첫단계에서 사용시 안해도 됨.
but 전처리를 직접 하는거 보단 성능 낮을듯
⇒ 실무에선 전처리 → batch norm 둘다 사용
6. Weight 초기화
📍 Xavier 출현배경 + Xavier에 대해
1) 방법 3가지 (모두 문제있음)
a. W=0, b=0으로 초기화
- 문제점
- 모든 output들이 0이되고, 모든 gradient가 동일해짐
= output은 input과 관련이 없어짐 ⇒ gradient =0이 돼서 totally stuck됨 - 대칭이 깨지지X (계속 같은 gradient 학습) → 학습 불가됨
- 모든 output들이 0이되고, 모든 gradient가 동일해짐
- b. small random 숫자들로 초기화*
-

- 문제점
- deeper network에서 문제 발생
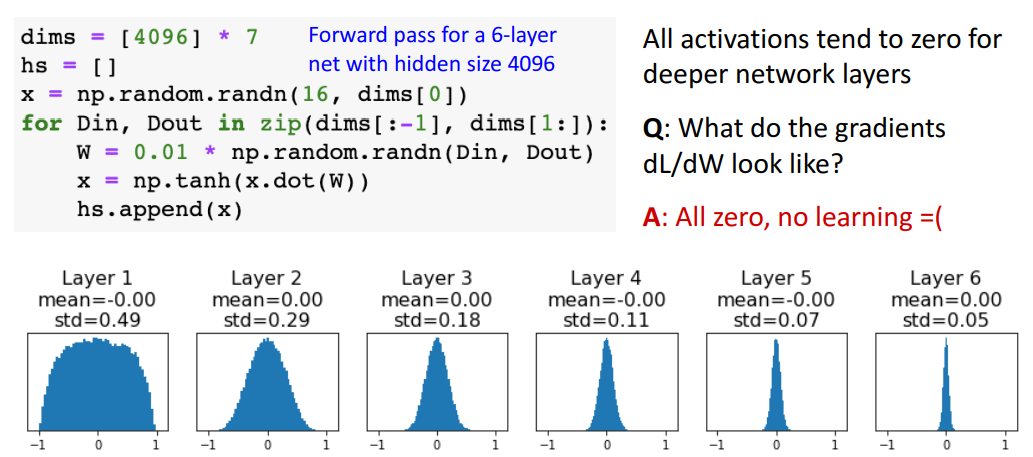
= local gradient들이 모두 0이 됨 → downstream gradient도 0이 돼서 학습 X- 증명
- 해석
- 각 6개의 layer의 hidden unit값들을 시각화한것
- hidden state = W가 Din, Dout의 사이에 small random값으로 초기화 되어 x와 내적한값
- 이 hidden state들의 기울기가 점점 0에 수렴하게 됨
- cf) weight의 local gradient = 이전 layer의 activation
- 결과
- cf) weight의 local gradient = 이전 layer의 activation
- layer가 깊어질수록 activations가 0에 수렴 (학습에 매우 bad)
⇒ local gradient들이 모두 0이 됨 → downstream gradient도 0이 돼서 학습 X
- 해석
-
- 증명
- deeper network에서 문제 발생
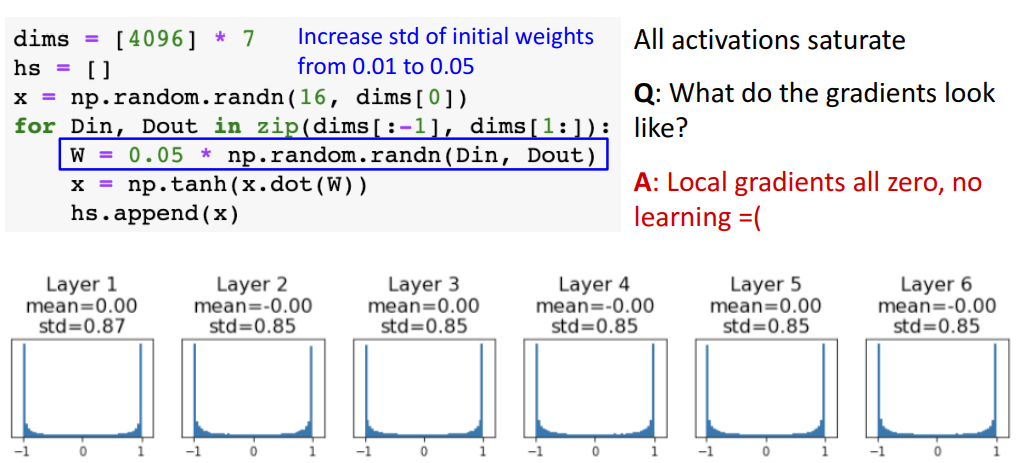
c. W를 조금 더 큰 숫자로 초기화
- 문제점
- local gradient들이 모두 0이 됨 → downstream gradient도 0이 돼서 학습 X
- 증명
- 해석
- tanh로 인해 극단값으로 밀려남
- 결과
- local gradient들이 모두 0이 됨 → downstream gradient도 0이 돼서 학습 X
- tanh로 인해 극단값으로 밀려남
- 해석
-
- 증명
- local gradient들이 모두 0이 됨 → downstream gradient도 0이 돼서 학습 X
2) 해결 방법
a. Xavier Initialization
- 방법
-

- **std = 1/sqrt(Din)**
- 하이퍼파라미터 X- 결과
- !

- layer가 깊어져도 ㄱㅊ음- conv layer에서 적용 방법
-

- 도함수
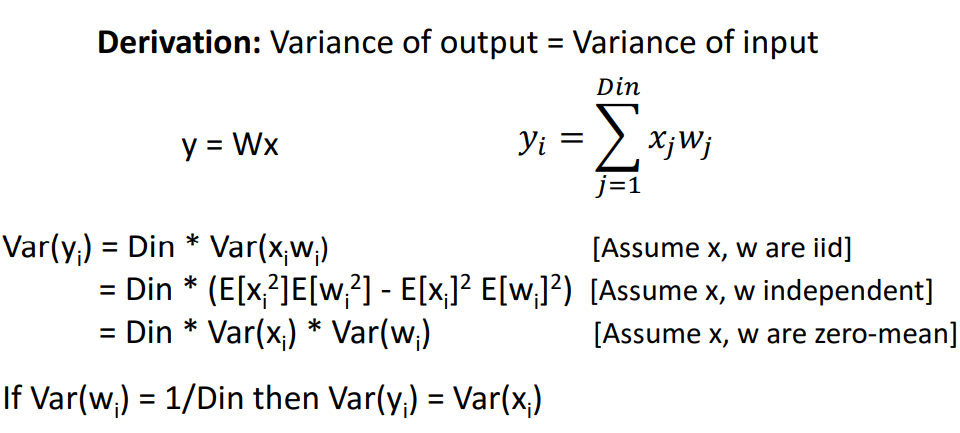
- Xavier의 목표
- output 의 activation 분산 = input의 activation 분산 하기!
(왜냐면 기존 초기화 방법들은 input과 output의 분산이 달라서 문제였어서) - 증명
-
- output 의 activation 분산 = input의 activation 분산 하기!
- Xavier의 목표
- **가정**
- x,w는 모두 가우시안 분포를 따른다. (0 분산)
- **결과**
- **Var($w_i$) = 1/Din 이면, Var($y_i$) = Var($x_i$)이다**
**⇒ 따라서 Xavier 초기화 = 1/sqrt(Din) 이 된 것.**- cf) ReLU로 input x와 W를 내적한다면?
-
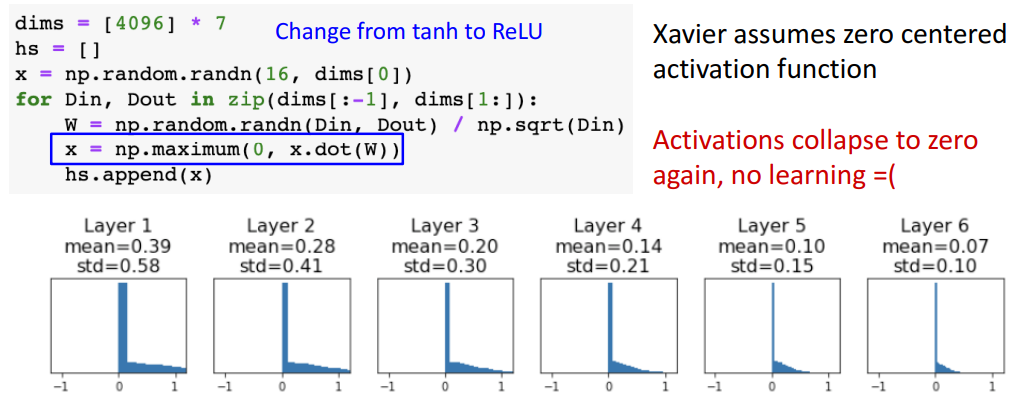
- **결과**
- **Xavier에서 relu 작동 X**
- 이유) Xavier는 x와 w가 zero-mean임을 가정하는데 relu는 그렇지 않아서 맞지 않음7. Weight 초기화 : Kaiming / MSRA 초기화
📍 relu그대로 사용대신, w초기화 방법 변경 → resnet에서 안맞는 부분 해결
1) 방법
- relu그대로 사용, 대신 weight초기화 변경
- (기존) std=1/sqrt(Din) → (변경) std=sqrt(2/Din)
- relu는 반을 죽이니까 걍 2배를 해도 됨 (뉴런의 절반이 죽을거라는 사실에 대해 조정)

2) 문제점
- VGG를 scratch 내면서 train 시킴 (지적받음)
- Residual Network에선 유용 X
-

- **이유: residual connection 이후의 output에 input을 다시 넣어서 분산, 분포가 엄청 클 것**
- ex. Var(F(x))(1번째 output에 대한 분산) **=** Var(x)(input에 대한 분산) *(여기까진 정상)*
Var(F(x)+ x)(2번째 output에 대한 분산) **>>** Var(x)(input에 대한 분산) *(residual로 input을 다시 넣어줘서 분산이 더 큼, 일치X)*
- **따라서, Xavier or MSRA에서 분산이 매우 크므로 → bad gradient → bad optimization**3) 해결책

- 첫번째 conv를 MSRA로 초기화
- 두번째 conv (last layer)를 0으로 초기화
⇒ Var(x+F(x)) = Var(x) 일치 가능
= 분산이 너무 커지지 않을수있음
4) 질문
- Q. (W 초기화 목적) 초기화의 idea가 손실함수의 global minimum에 도달하기 위함인가?
A. 아님, train 전엔 그 minimum이 어딘지 모름, 대신 모든 gradient가 초기화를 잘 행할 수 있도록 하는 것
= 잘못된 초기화 하면 zero gradient가 되어버릴 수 있어서
= lost landscape에서 flat한 곳에서 시작하여 걸어가지(train) 않도록 도와주는 작업
8. Regularization : Dropout
1) 사용 목적
- 과적합 방지
-
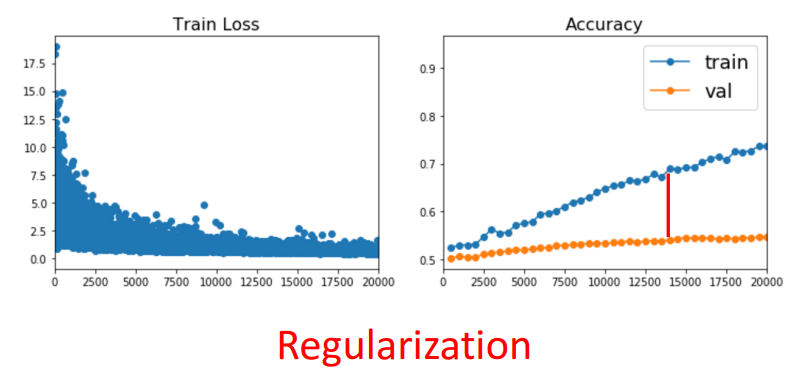
2) 방법
a. Loss뒤에 $\lambda$$R(W)$ 붙이기
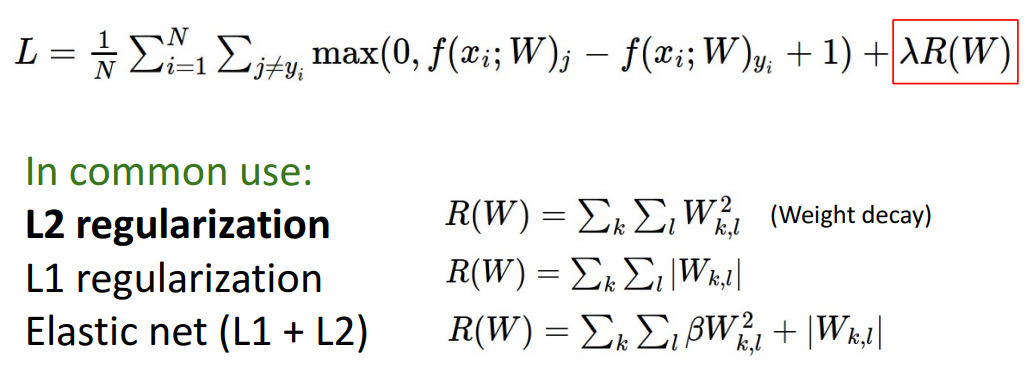
- L2 norm → 젤 사용 多
b. Dropout
- 방법
- 각 layer마다 순전파 시, 랜덤하게 몇몇 뉴런들을 0으로 세팅
- 얼마나 drop할건지는 hyper parameter임; 0.5가 일반적
-
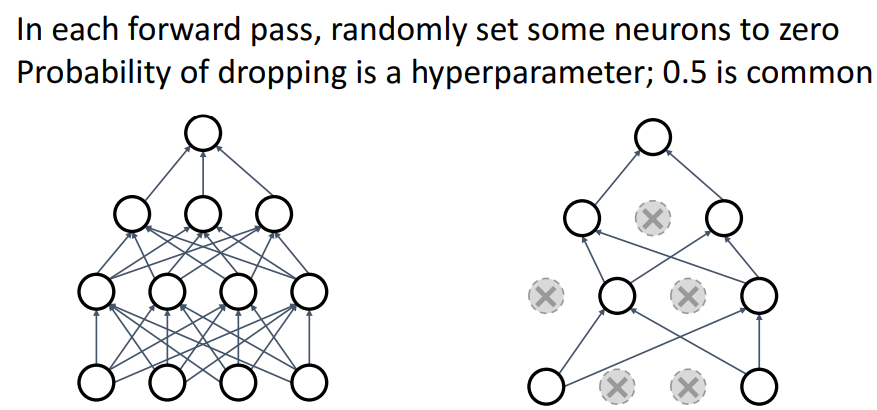
- 구현하기
-

- Dropout하는 이유 2가지
- 중복 적용하는 것 방지
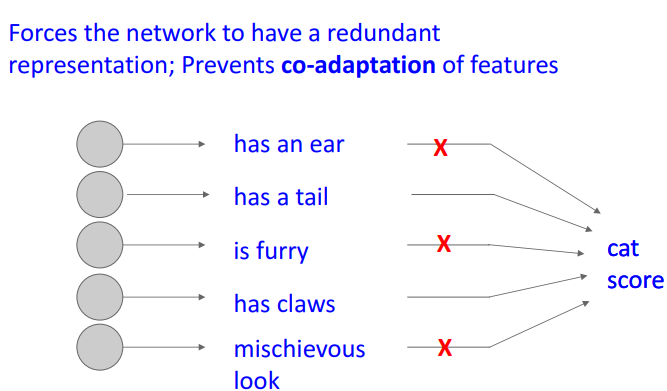
- x의 feature잘 학습 위해, 필요없는 feature 덜 배우고 중복 노드 배우는걸 방지
- ⇒ 결론) 과적합 방지*
- 앙상블처럼
-
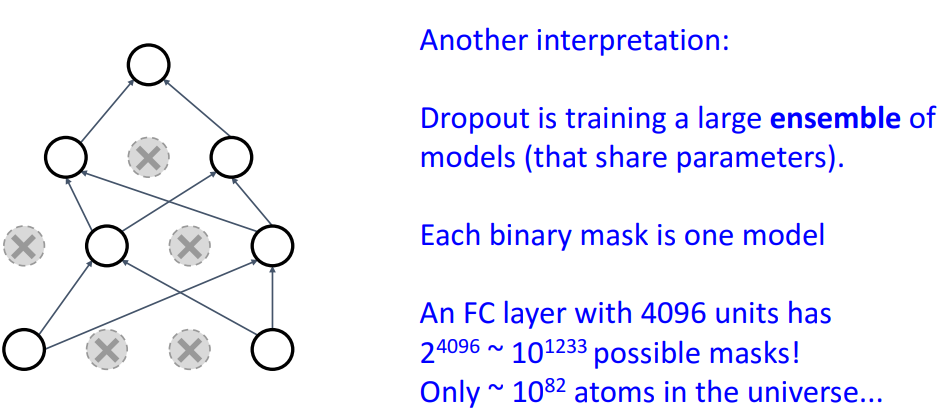
- 중복 적용하는 것 방지
- Dropout은 파라미터 공유하는 **여러 Neural Network 앙상블 training**
- 여러 submodel 만들어서, **앙상블처럼 최종 결론 투표 결정**- Test Time에서의 Dropout
- 문제점
-

- **z**=random변수 (순전파 이전에 정함)
- **결론) test시, random하게 뉴런을 끄게 되면 test마다 결과가 다 다르게 도출**
이유) 각 forward pass마다 random하게 뉴런 떨어트려서
- **해결책**
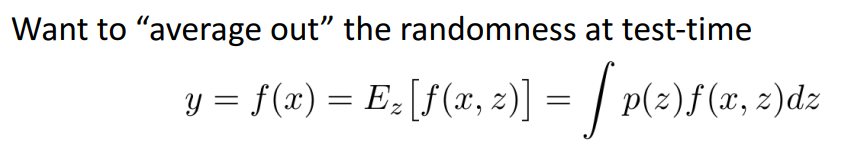
- 이러한 randomness (**z**) 를 **평균**내자!
- **해결방법**
- **위의 integral 근사화 하는 방법**

- ***(dropout시)* 4개의 각기 다른 train시에 만들어진 random mask들 곱해짐**
→ **z** (random 변수)에 대해서 평균내는 것
- **구현**

- **방법**
- test time에선 모든 뉴런들 사용
- **but 각 뉴런을 drop할때 dropping 확률(p) 써서 layer의 output을 rescale함**- 결론(전체 구현)
-

- **train**: 걍 그대로 dropout
- **test**: 적절한 확률(p) 사용해서 output을 rescale하고, randomness없앰
- *각 개별 layer에만 적용 가능*
- *stacking multiple dropout layer시 사용X*- 일반적인 구현 방법 (Inverted Dropout)
-

- 일반적으로,, **train**시 drop & scale 모두 함(뉴런을 1/2개 dropout시키고 남은 뉴런들을 2배함 )
**test**시에 모든 뉴런 사용 + 모든 normal weight matrix 사용9. Dropout architectures
📍 Dropout이 아키텍처들에 어케 쓰이는지
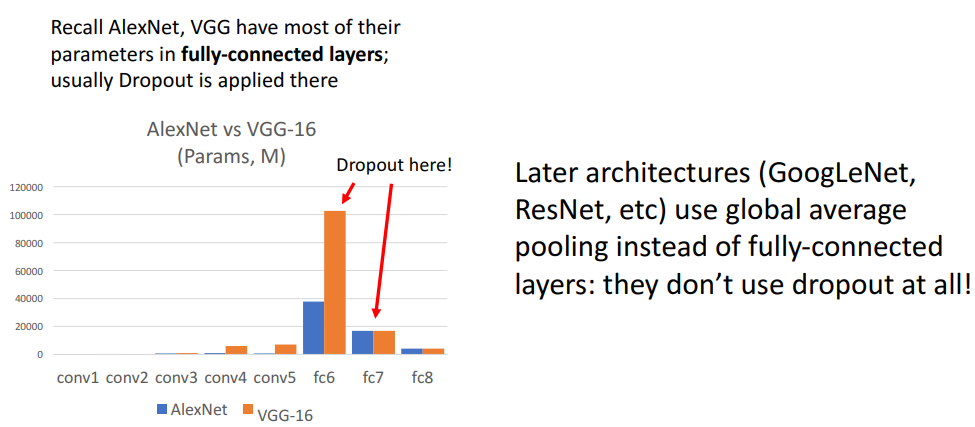
- 결론
- AlexNet, VGG : 맨 윗단 레이어인 FCLayer에서 dropout적용
- 이외 최신 아키텍처: FCLayer를 줄였기에, dropout 사용할일 거의 없음
10. Regularization : A common pattern
- Batch norm
-
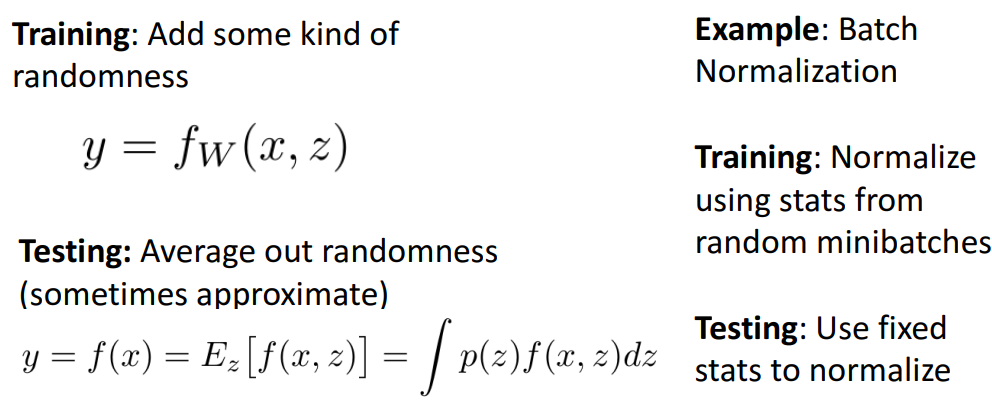
- 최신 아키텍처에는…
- dropout 사용X
- → 대신 batch norm or L2 정규화
11. Regularization : Data Augmentation
📍 좌우대칭, 밝기조절 등
- 개념
-
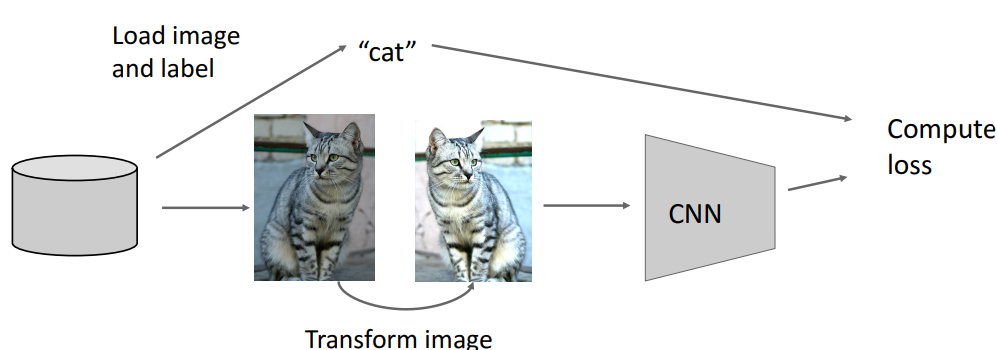
- 방법
- Horizontal Flips (좌우 대칭)
-

12. Regularization : Drop Connect
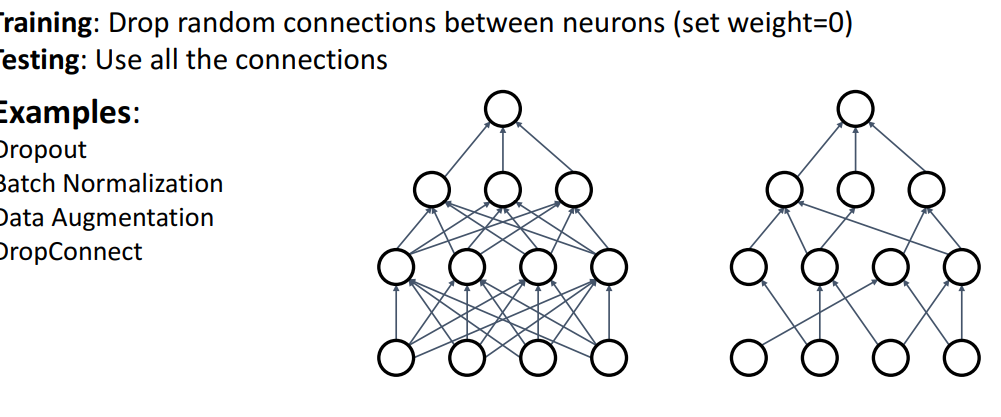
13. Regularization : Fractional Pooling
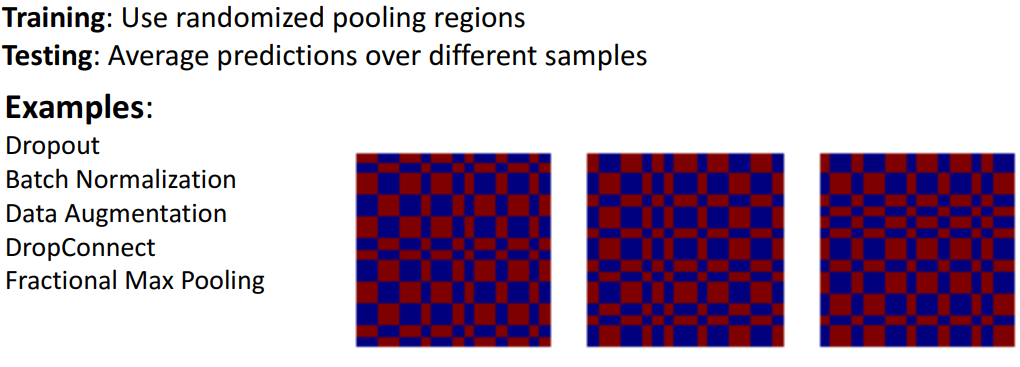
14. Regularization : Stochastic Depth

15. Regularization : Cut out

16. Regularization : Mix up

'2023 딥러닝 > Michigan University DL' 카테고리의 다른 글
| [EECS 498-007 / 598-005] 12강: Recurrent Neural Networks (0) | 2024.02.27 |
|---|---|
| [EECS 498-007 / 598-005] 11강: Training Neural Networks (Part2) (2) | 2024.02.27 |
| [EECS 498-007 / 598-005] 8강: CNN Architecture (1) | 2024.02.27 |
| [EECS 498-007 / 598-005] 7강: Convolutional Neural Network (0) | 2024.02.27 |
| [EECS 498-007 / 598-005] 6강: Backpropagation (0) | 2024.02.27 |