📌 본 내용은 Michigan University의 'Deep Learning for Computer Vision' 강의를 듣고 개인적으로 필기한 내용입니다. 내용에 오류나 피드백이 있으면 말씀해주시면 감사히 반영하겠습니다. (Stanford의 cs231n과 내용이 거의 유사하니 참고하시면 도움 되실 것 같습니다)📌
(📁 아래에 똑같이 제가 정리해놓은 블로그 참고..! 벨로그에 있는게 더 깔끔히 정리 잘되어있습니다)
https://velog.io/@ha_yoonji99/Michigan-Univ-DL-7%EA%B0%95-Convolutional-Neural-Network
[Michigan DL/cs231n] 7강: Convolutional Neural Network
🔥Michigan University Deep Learning 7강🔥
velog.io
0. LastTime: Back prop
- 기존 문제점) 일반 선형분류 or fully connected network는 입력이미지의 2D공간 구조 존중X
- 무조건 1D로 바꿨어야됨
- 해결책) 이미지, 공간구조 다룰줄 아는 operator 새로 정의하면됨
1. 구성 요소
1) Fully Connected network

2) Convolutional Network
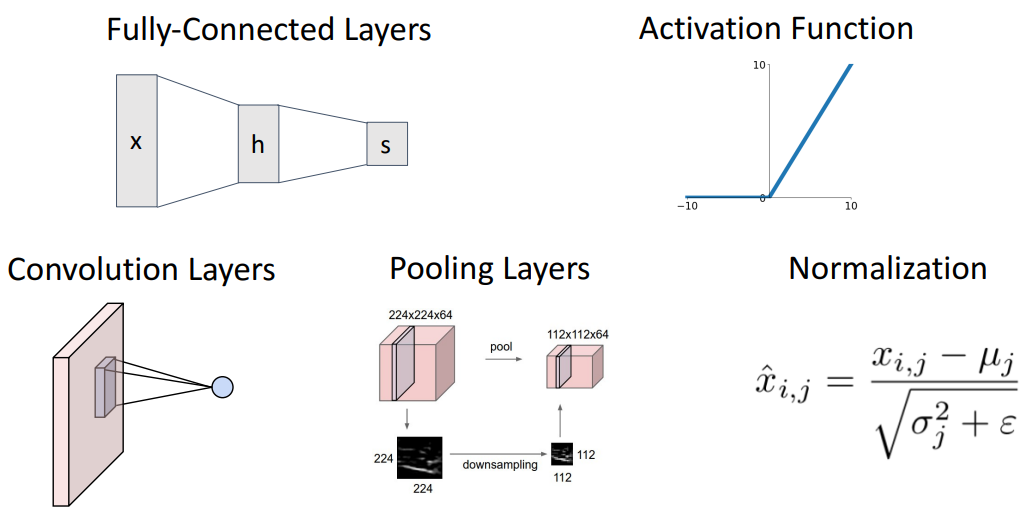
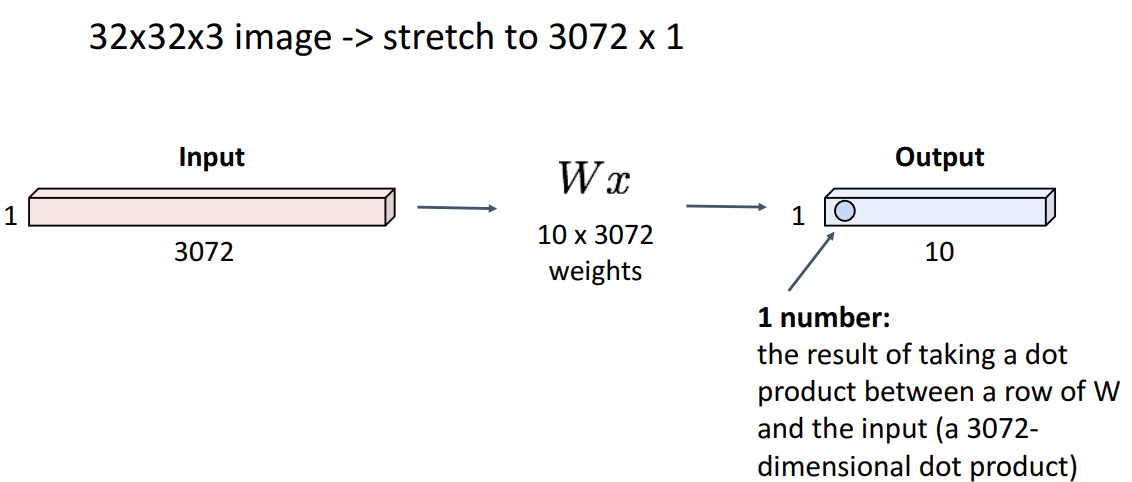
2. Fully Connected Layer
- 벡터화
3. Convolution Layer
📍filter가 weight역할 해줌(input에 대한 영향력 전달)
1) 구조

- input volume
- 3차원 (3x32x32) (RGB x Height x Width)
- filter
- weight matrix와 동일 역할
- filter의 RGB와 input의 RGB맞추는것 중요!
- input image의 모든 공간위치로 슬라아드하여, 또 다른 3차원 계산
- 입력 tensor의 전체 깊이에 걸쳐 확장됨
2) first filter
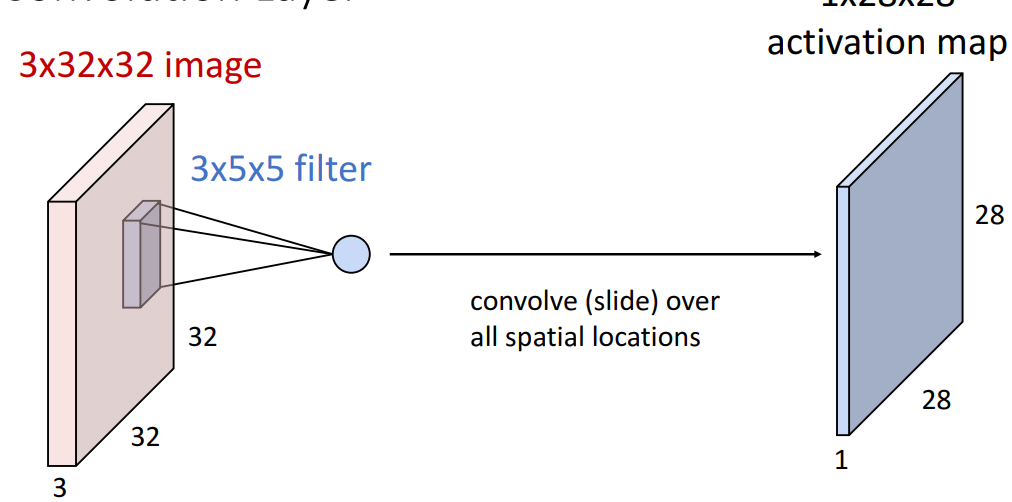
- filter
- input image의 내부 어딘가에 붙임
- input tensor의 일부 공간 위치에 할당
- ⇒ input tensor와 filter 사이의 내적곱 진행
- output
- 1개의 element (single number)
- 1개의 filter와 input tensor의 작은 local chunk 계산
- input image의 이 위치가 하나의 filter와 얼마나 일치하는지 효과적으로 알려주는 단일 스칼라숫자 계산
3) second filter
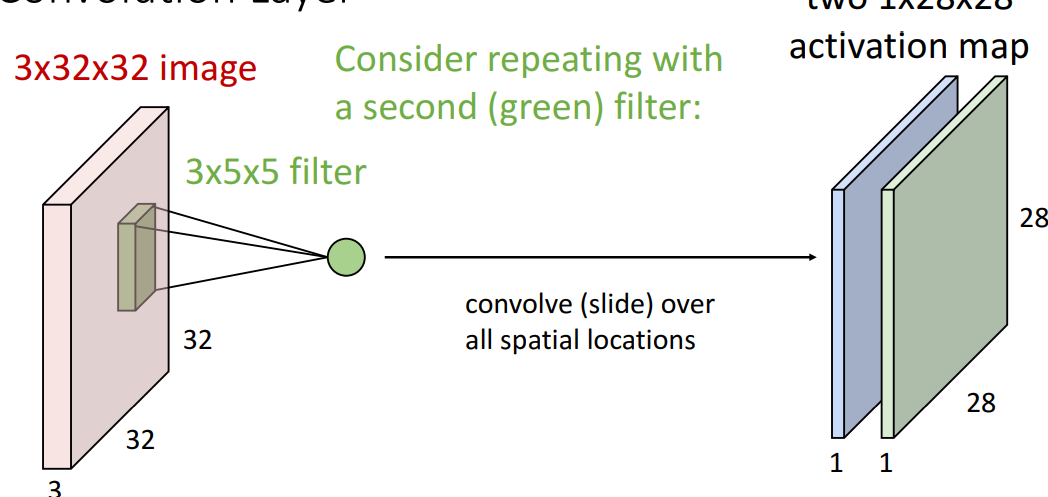
- activation map
- filtering한 결과를 부르는 다른 말
- green filter
- 앞과 weight값이 다른 filter
4) 여러개의 filter
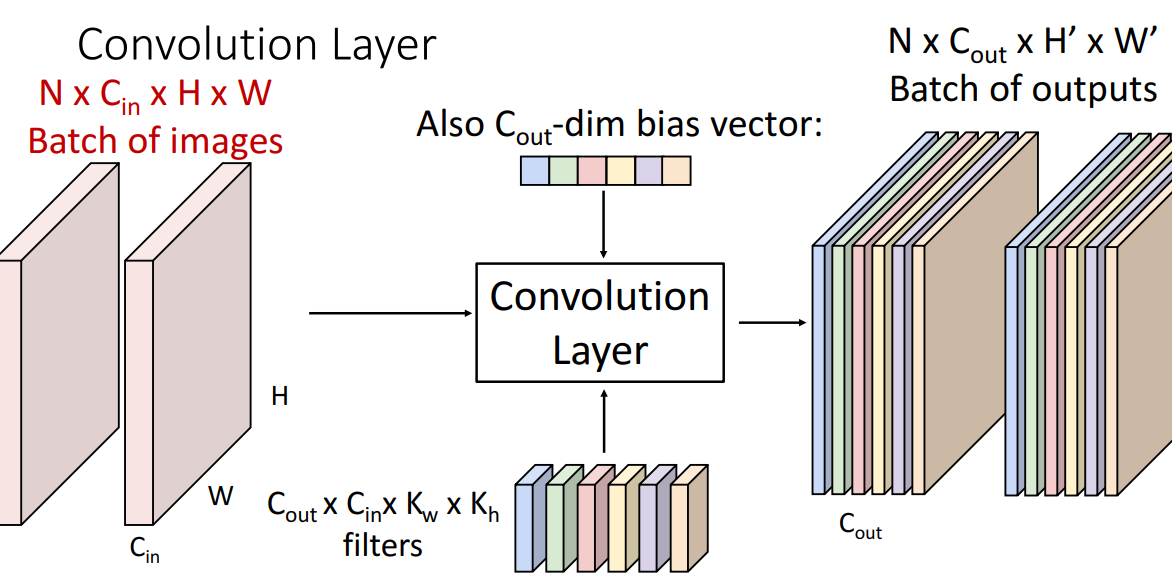
- 여러 filter (6x3x5x5)
- 집합 6개의 3차원 필터
- 6 x 3 x 5 x 5 = filter수 x input channel수 x (filter크기)
- 6개의 activation map 나옴
- stack activation maps (6개)
- 크기는 달라졌지만 첫 input과 같은 3차원 공간구조 보존
- 해당 필터에 대한 전체 입력이미지의 응집정도 나타냄
- 합성곱층의 출력의 공간구조 생각 가능
- 28 x 28 grid
- 입력 tensor의 동일 공간 grid에 해당 (각 위치에서 합성곱층은 특징벡터 계산)
- 6-dim bias vector
- 원래 하나의 filter당 1개 bias있음
- 총 6차원(vector) bias 있는 것
5) 3차원 tensor batch
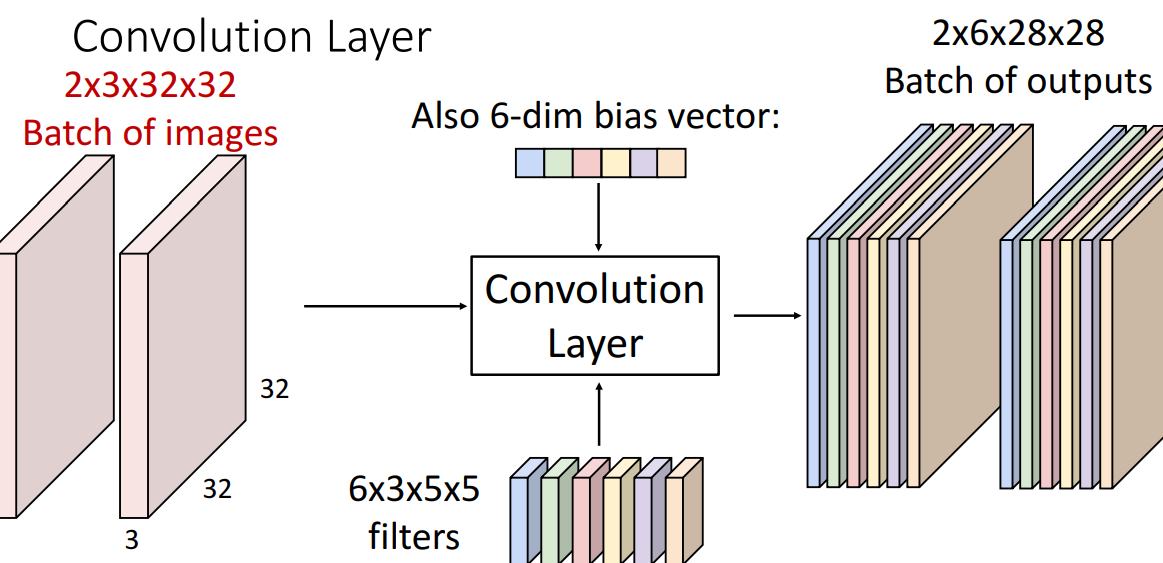
6) 일반화
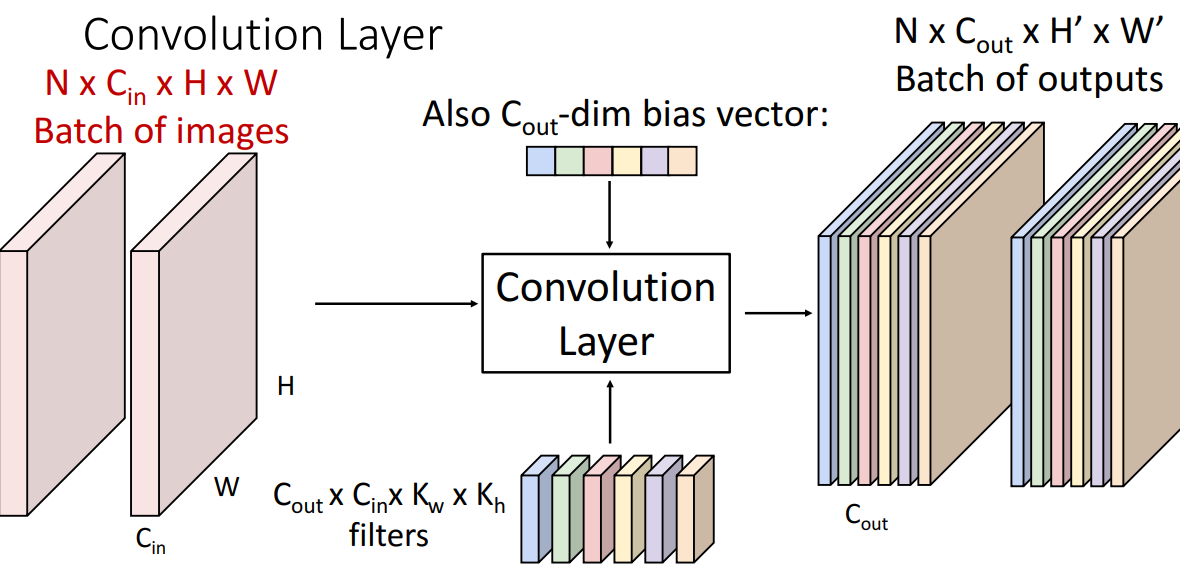
- input
- N x Cin X H x W = (개수 x batch의 각 입력image에 있는 채널수 x 각 입력 요소의 공간 크기)
- output
- N x Cout x H’ x W’ = (개수 x filter개수(Cin과 다를수있음) x input image의 H,W와 다를수O)
4. Stacking Convolutions
📍filter(conv)뒤에 활성화함수 넣어서 선형 극복
- Convolution layer를 stacking가능 (더이상 fully connected layer X)
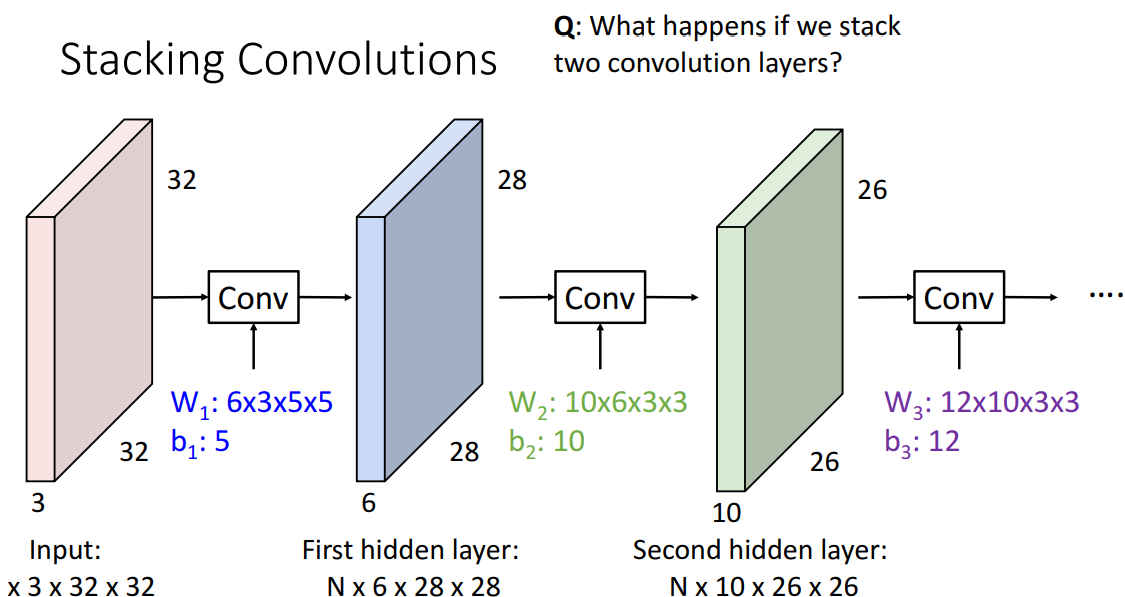
- 해석
- input
- 3차원 tensor batch N개
- W1 : 6x3x5x5
- 의미: 6개의 convolution filter
- Nx3x32x32
- 부르는 이름: 3 layer CNN with input in Red, first hidden layer blue, second hidden layer green
- input
- Q. 2개 convolution layers stack하면 어케됨?
- 각 convolution 작업자체가 linear 연산자이므로, 하나의 convolution을 또 stack하면, 또 다른 합성곱 만들어짐
- ⇒ 극복) 각 선형 연산 사이에 비선형 활성화함수 삽입*
- (fully connected layer같이 3차원 tensor의 각 요소에 대해 작동)*
-
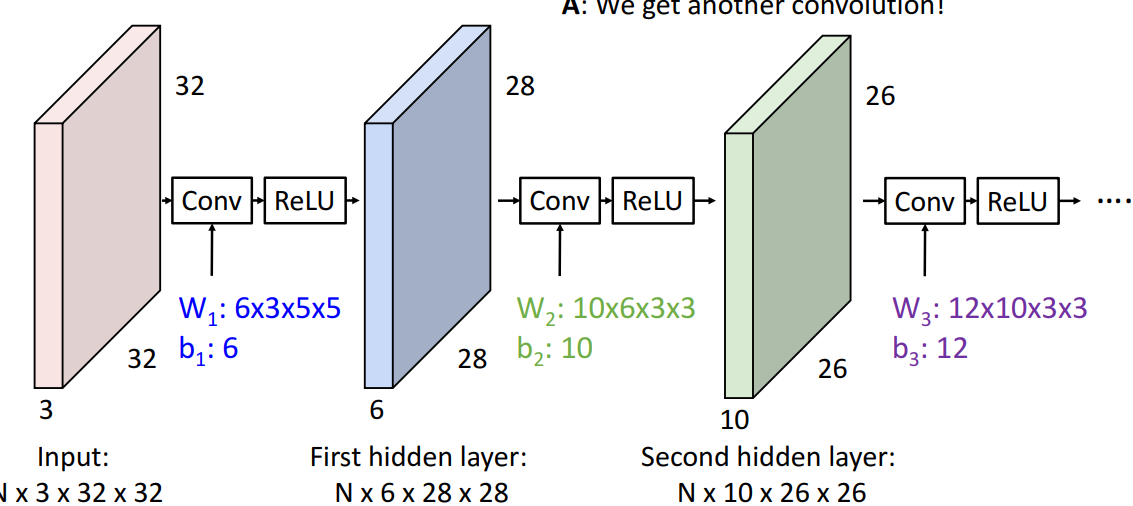
- A. 또 다른 convolution 얻음 (y=W2W1x도 여전히 linear classifier임)
5. 학습가능한 convolutional filter
📍MLP: 모든 이미지 template을 학습함- 1번째에서는 모서리 위주
1) 기존 linear classifier
- conv filter가 뭘 학습하는가? → one template per class (1차원만 가능해서)
-
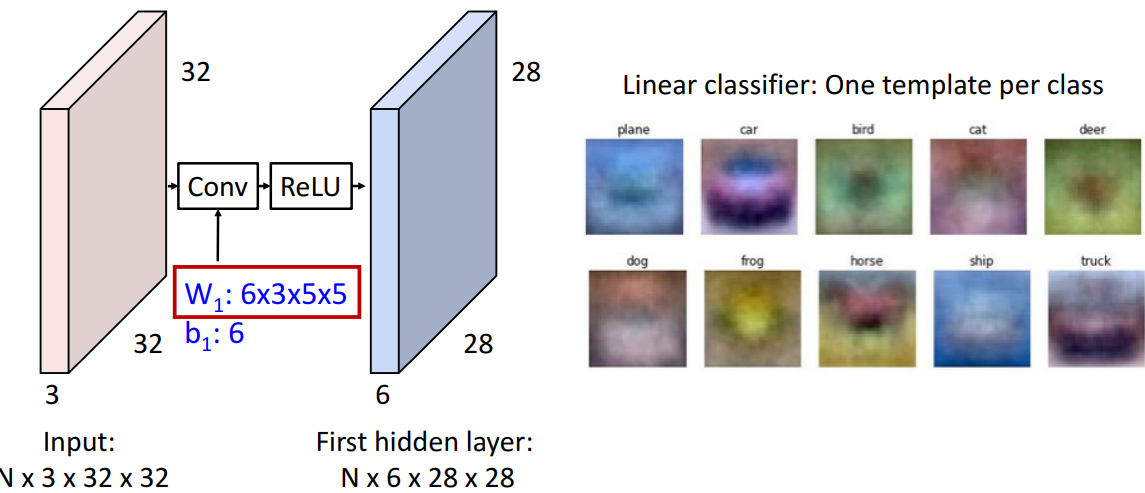
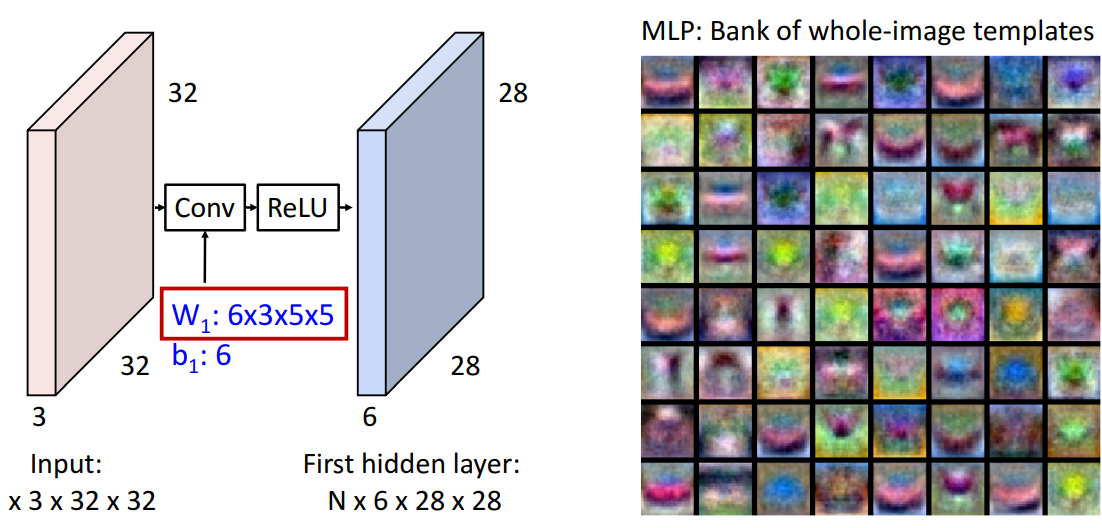
2) MLP
- conv filter가 뭘 학습하는가? → Bank of whole image templates (다차원도 가능해서)
- fully connected: 입력 이미지의 전체 크기에 걸쳐 확장됨
= fully connected network와 1번째 layer는 각각 입력 이미지와 동일 크기를 갖는 template bank 가짐 -
3) First layer conv filters
- conv filter가 뭘 학습하는가? → local image templates (모서리, 반대 색 학습)
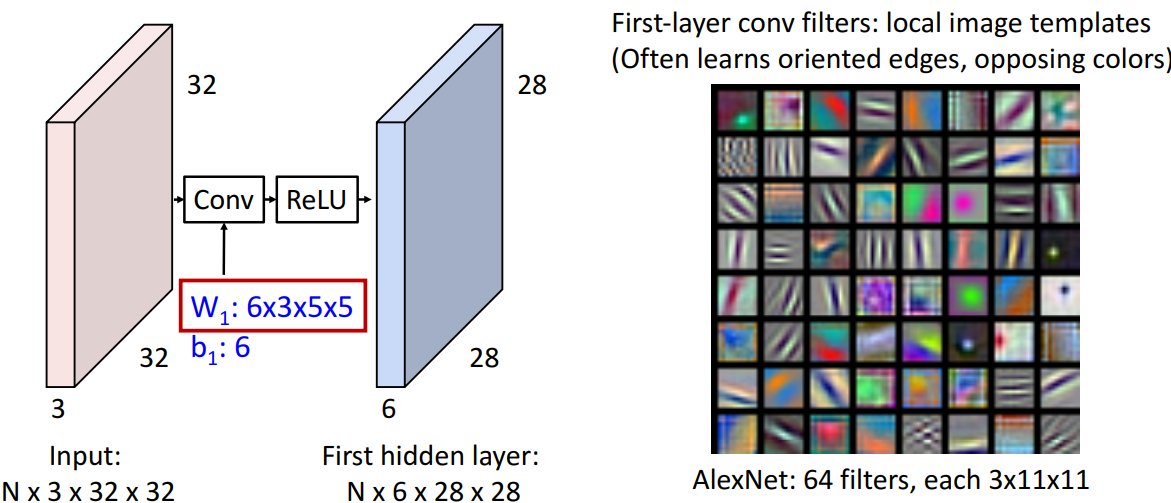
- ex. green blob next to red blob
- image의 반대 색상을 찾고있다는 것
- 1번째 convolution 연산후 2번째 feature이 뭔지에 대한 해석은 해당 3D 출력 tensor에서 각 활성화 map이 각 위치의 정도 제공
- 해당 chunk가 1번째 layer에서 학습된 각 template과 얼마나 일치하는지 (ex. 합성곱 네트워크의 1번째 층에서 학습된 이러한 필터들과 유사효과)
6. Padding
📍기존: W-K+1 → 패딩후: W-K+1+2P
- 깊이, 채널 고려X
1) 기본
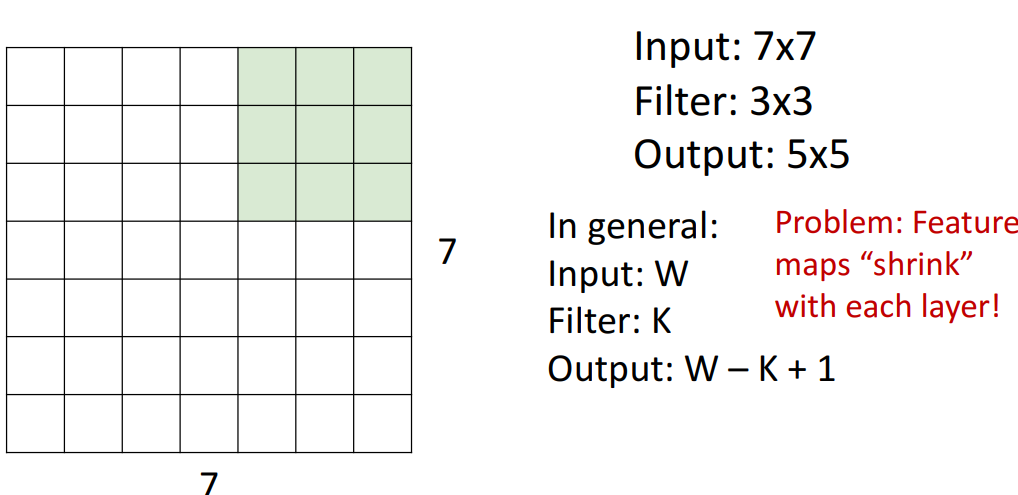
- 출력크기 (일반화)
- : W-K+1
- 문제점
- : feature map이 각 layer마다 줄어듦(공간 차원이 줄어듦)
2) 해결책: 패딩
- zero-padding
-
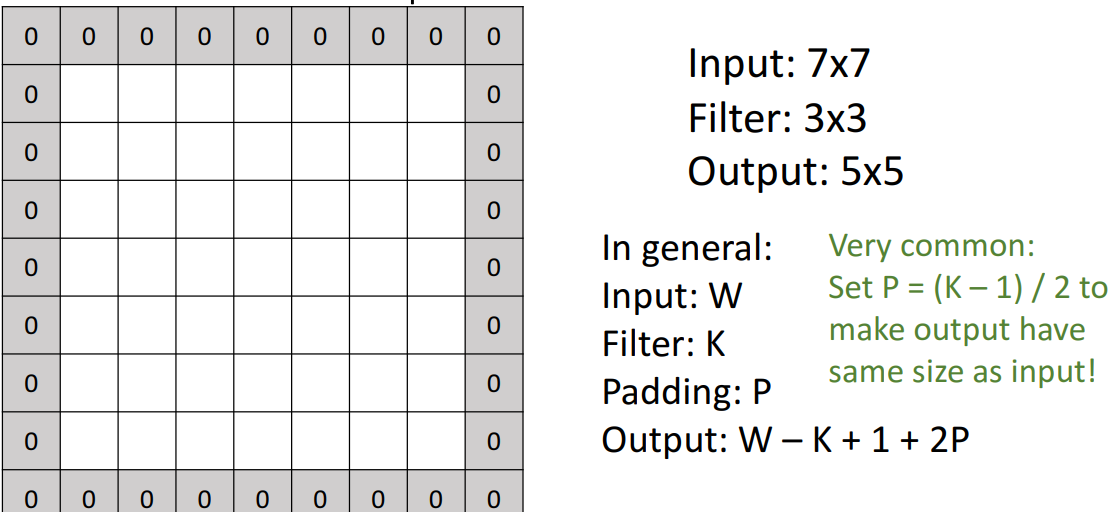
- 패딩 추가 후
- output 일반화 식
- : W-K+1+2P
- Same padding
- 입출력이 동일 공간 크기 가져서 → 공간 크기 추론이 쉬워짐
7. Receptive fields
1) 1개의 conv layer 적용
(1) (2)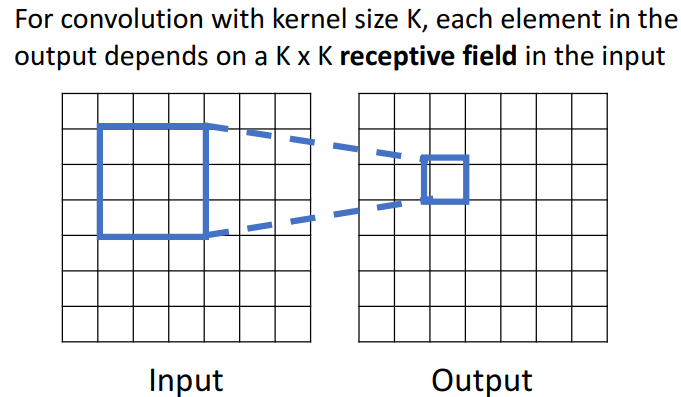
- 해석
- output image의 각각의 공간 위치는 input image의 local region에만 의존
- ex. 2는 1의 영역에만 의존
- 1의 영역: receptive field of the value of output tensor
2) 여러개의 conv layer를 stack
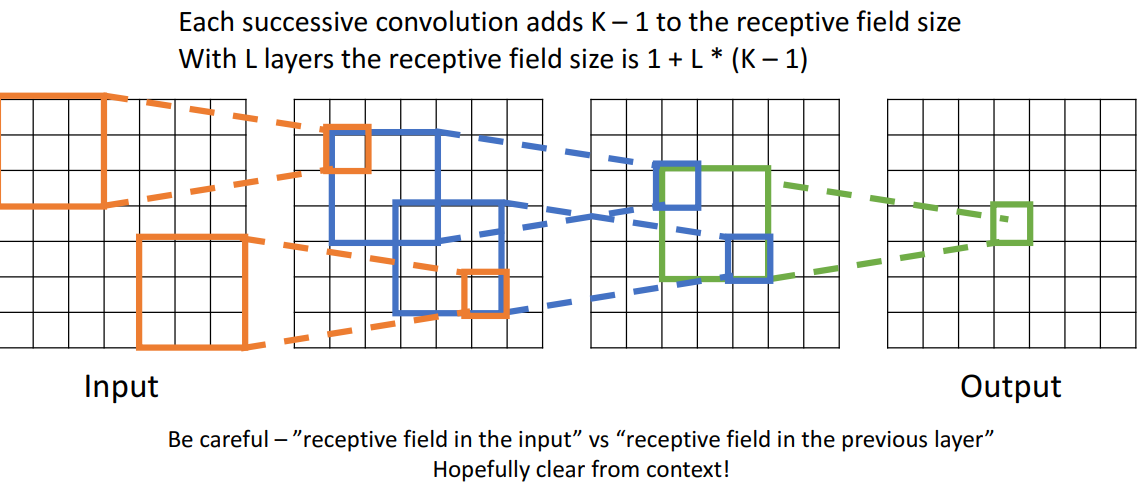
- 해석
- 녹색 영역은 전이적으로 맨 왼쪽 input tensor의 주황부분의 공간에 따라 달라짐
- 2가지 해석
- receptive field in the input: 여러개의 합성곱층 거친 후, 해당 뉴런 값에 영향 미칠수있는 input image의 공간 크기
- receptive field in the previous layer: 이전층의 영향
- 문제점
- 매우 높은 해상도 이미지로 작업하려면 → conv layer많이 쌓아야됨
= 매우 큰 receptive field 유지위해 엄청 많은 conv layer 쌓아야됨
- 매우 높은 해상도 이미지로 작업하려면 → conv layer많이 쌓아야됨
- 해결책
- stride 써서 downsampling하기
8. Stride convolution
📍receptive field 더 빨리 구축 → ((W-K+2P)/S)+1)
1) Stride
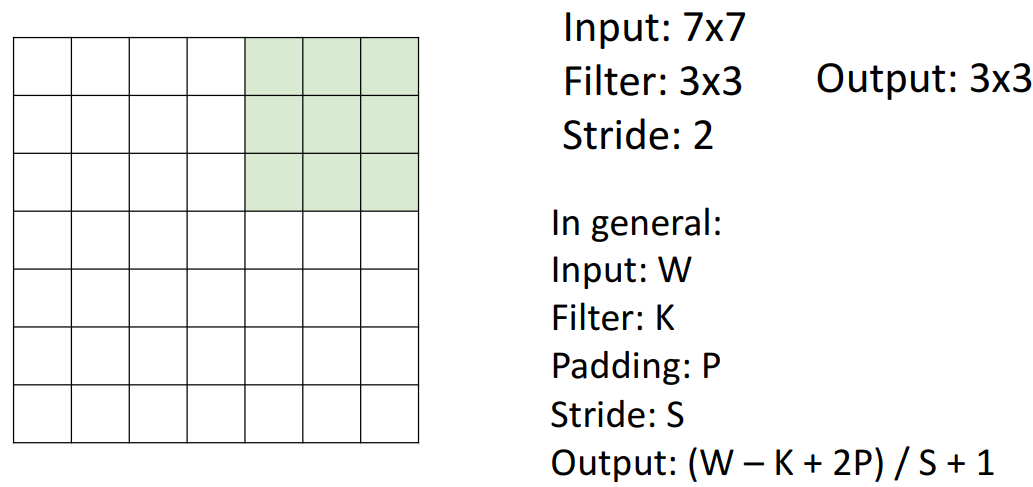
- 개념
- 가능한 모든 위치에 conv filter 배치하는 대신, 가능한 N의 위치마다 배치
- ex. stride=2 → output=3x3
- output
- downsample됨
- receptive field를 더 빨리 구축가능
- 모든 layer에서 receptive field가 2배가 되기 때문
- ((W-K+2P)/S)+1
9. Recap: Convolution Example
📍걍 일반화 식들 정리
1) output volume size?

- 주의점
- output은 filter 개수와 동일해야됨 !!!!
2) Number of learnable parameters?

- 일반화 식
- filter 개수 * (channel수filter크기(kk)+1(bias))
3) Number of multiply-add operations?

- 일반화 식
- output volume size * 1filter
4) example: 1x1 convolution
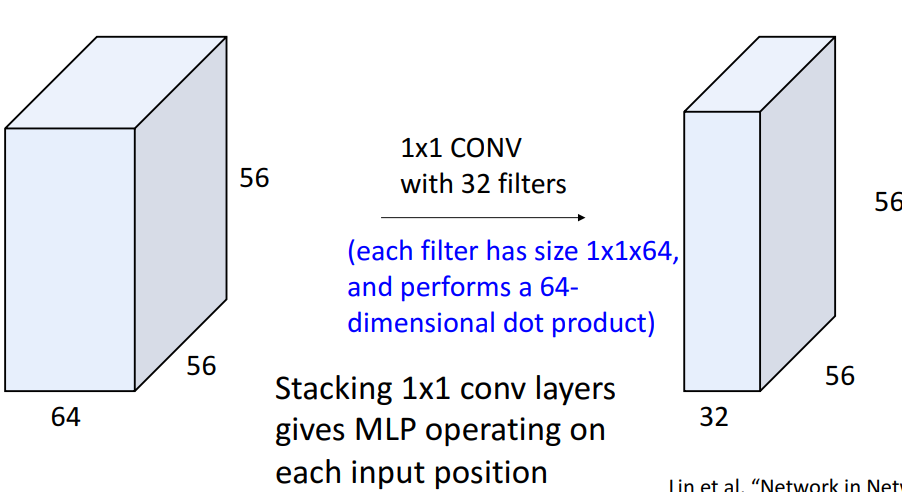
10. Convolution Summary

- 비교
| fully connected layer | 1x1 conv layer |
|---|---|
| 공간구조 파괴 : 전체 tensor 하나로 평면화 → 벡터 출력 | 공간구조 유지 |
| : 신경망 내부의 adapter 사용 |
11. Other types of convolution
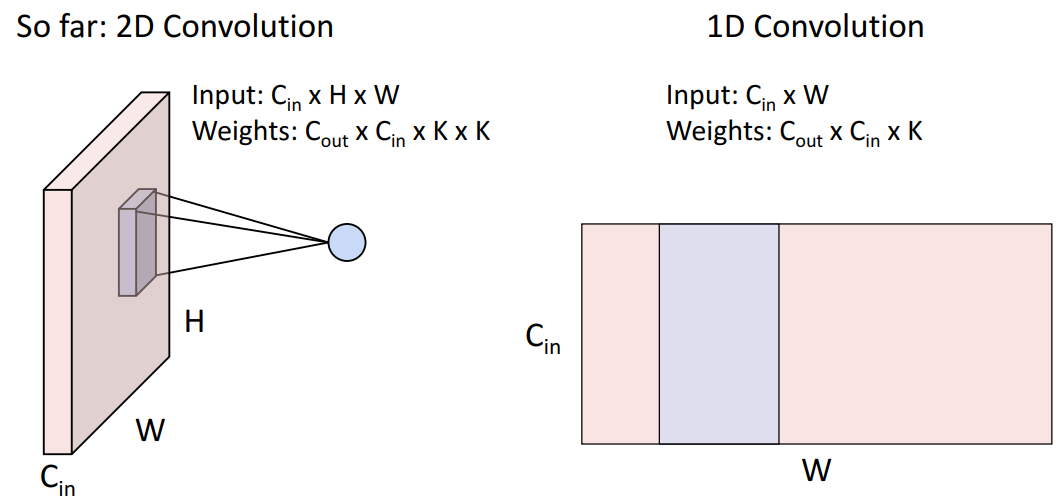
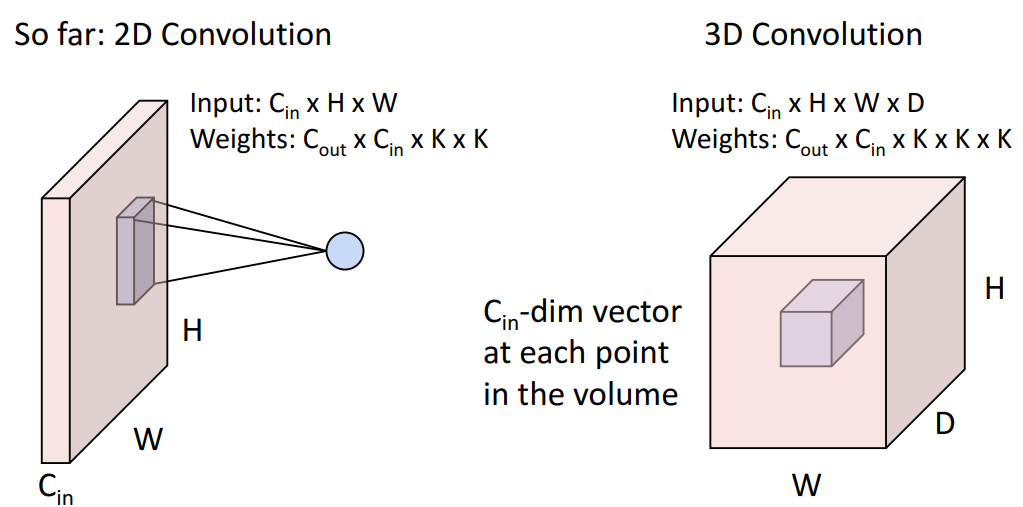
12. Pooling Layers
📍pooling더 쓰는 이유: 학습파라미터X, 값이 안변함
- 개념
- 학습 매개변수(파라미터) 없음
-
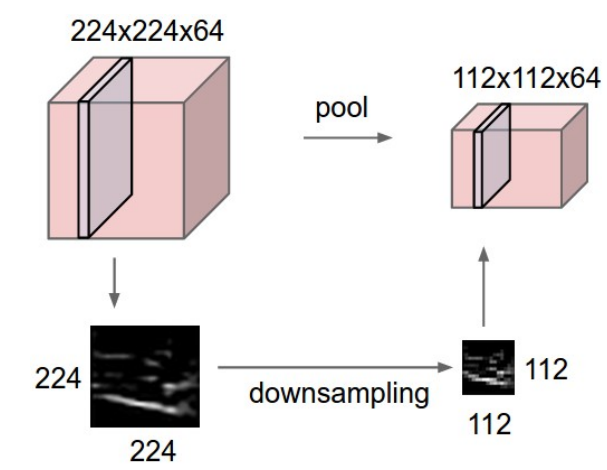
- 파라미터
- kernel size
- stride
- pooling function
- Max pooling
-
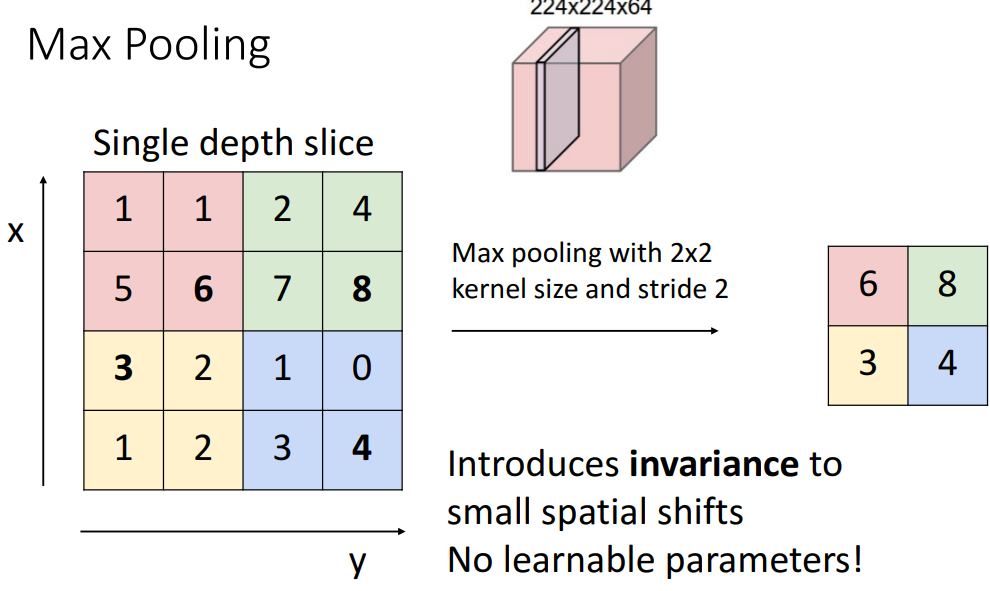
**a. Max pooling with 2x2**
(= kernel size (2,2) & stride=2)
→ kernel size = stride면 중첩되는 영역X
**b. pooling이 stride보다 더 많이 쓰이는 이유**
- **이유1)** max pooling같은 경우, 변환에 일정량의 불변성 있음**(해당 구역에서 값이 안변함)**
- **이유2) learnable parameter없음**- pooling summary
-

13. 앞서 배운것들 결합한 Convolutional Networks
1) 기본 CNN 구조
- 앞서 배운것들 연결하는 방법 많음
- 하이퍼파라미터가 있어서
2) 예시: LeNet-5
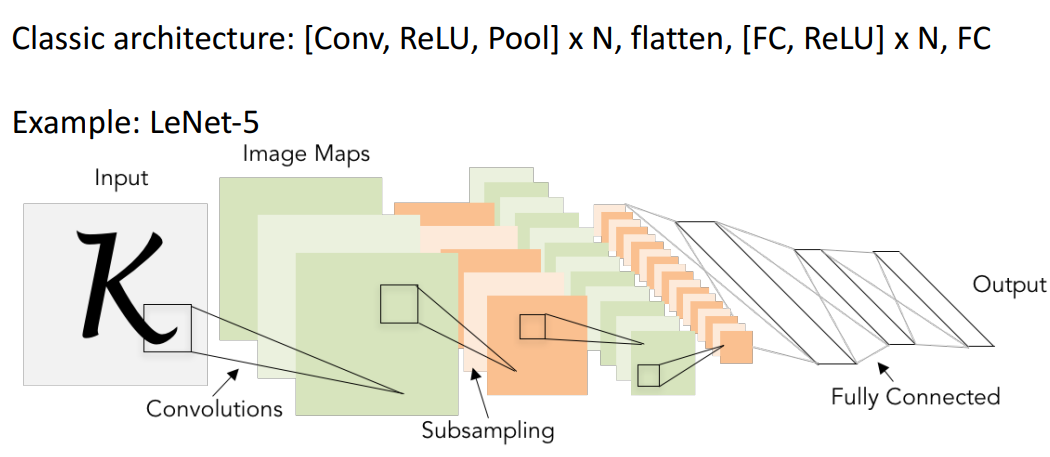
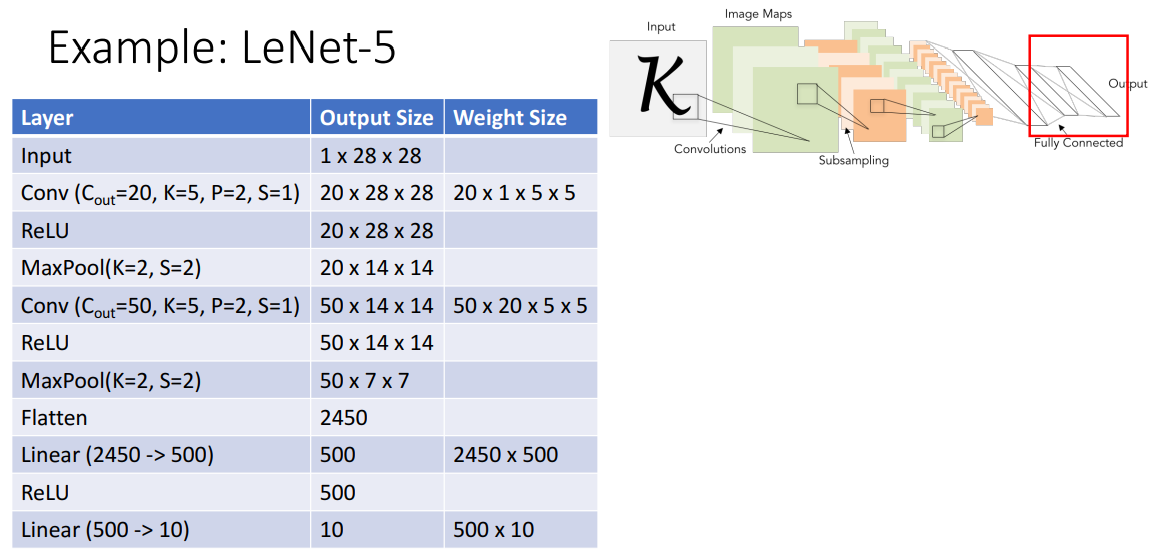
- 해석
- conv후에 relu넣는게 일반적
- Q. maxpool로 비선형하게 만들수있는데 왜 relu함?
- A. 걍 relu넣는게 일반적 (더 많은 규칙성 제공)

14. (Fully connected Network에서) Batch Normalization
📍선형적으로 할수있음
1) 개념
- 네트워크 내부에 일종의 layer추가하여 deep network를 train할수 있도록
- (평균=0, 단위분산분포 있도록) 이전 layer로부터 나온 결과를 어떤 방식으로든 정규화하기
2) 왜 정규화해야됨?
- internal covariate shift (ICS) ↓ → 학습 과정 안정화, 최적화 ↑
- ICS: 학습과정에서 각 층의 입력 분포가 변하는 것 의미
- 일반적으로 신경망에서 학습이 진행될수록 가중치, 편향이 업데이트 되고, 이는 각 층의 입력 데이터에 영향줌
→ 이로 인해 이전 층에서 학습한 표현들이 변경되어 다음 층에 영향 미치게 됨 - ICS는 학습의 안정성, 속도 ↓시킴
3) Batch Norm 식
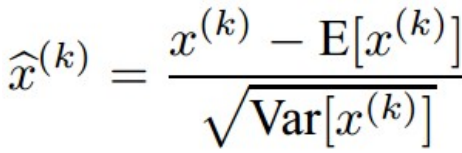
- backprop에 사용이 어케되냐
- 미분 가능 함수여서 gradient를 전달해줄수O
4) 특징
- (ICS제거 위해) 각 layer의 입력 feature 분포를 re-centering, re-scaling
- 각 layer마다 input의 분포가 달라지는 것 방지
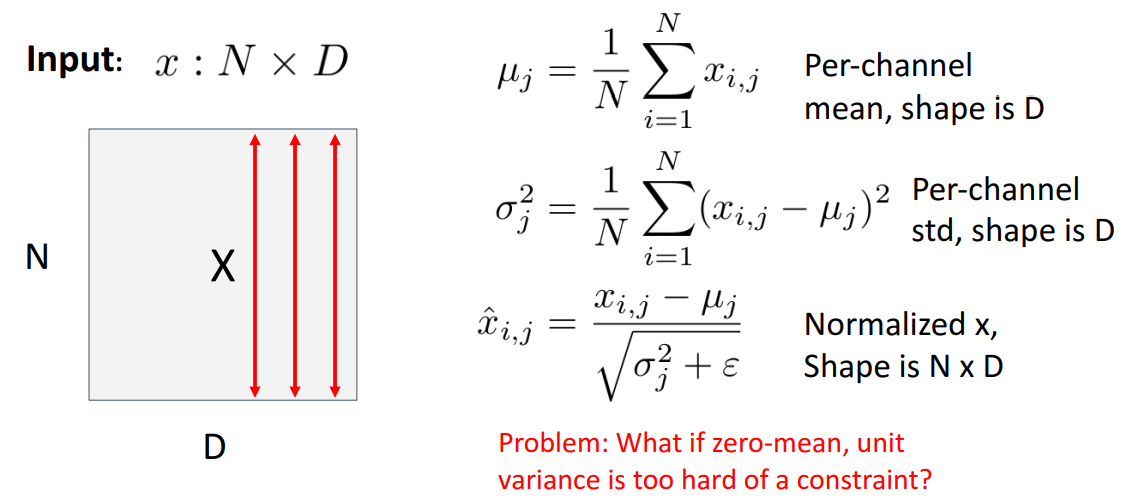
- batch ↕
- 각 벡터의 평균값
- 첫번째 식
- 채널별 평균값
- 두번재 식
- 채널별 분산
- 세번째 식
- 1,2번째 식 가져와서 정규화
- e : 0으로 나누지 않기 위함(작은 상수)
- zero centered 됨
- 문제점 (학습 파라미터를 넣는 궁극적 이유)
- Q. zero mean일때, 제약이 많이 걸리지 않을까?
- 해결책
- 기본 정규화 후 추가 작업(학습가능 파라미터 넣기) 필요
-

⇒ identity function 을 커버해줌5) 학습 시 batch normalization
- 최종 batch normalization 식
-
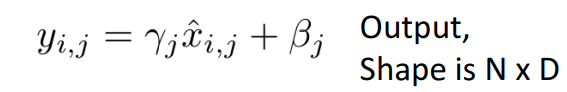
- $\hat{x}_{i,j}$ : 정규화된 input
- $y_{i,j}$ : 벡터의 각 요소에서 보고자하는 평균, 분산이 뭔지 스스로 학습 가능6) 검증(test)시 batch normalization
a. 문제점
- 다른 input 넣었는데, 넣는 것이 달라도 점수 같아버림
- 같은 input 넣었는데, output이 달라져버림
- ex. 고양이 사진 넣었을때의 점수와, 강아지 사진 넣었을때의 점수가 같아버릴때
- ex. 웹서비스에서 동시에 고객이 같은 자료 업로드했는데 output이 다를때
-

b. 해결책
- 배치의 요소에 대해 모델이 독립적이여야됨 (= train과 test 둘다에서 성능 좋아야됨)
- train 시에는 경험적으로 하지만, test에서는 그렇지 X (= batch에 기반하여 계산X)
- 방법
- train
- 모든 새로운 벡터와 시그마 벡터의 모든 평균 중 일부 실행 중인 지수 평균 추적
- test
- batch 요소 사용하는 대신, $M_j,$ $\sigma$ 같은 고정 scalar 될것 (상수)
- test 시간 배치의 요소간에 독립성 회복 가능
- train
- 수식
-

15. (Convolutional Network에서) Batch Normalization
📍장점(train쉽게, LR높게,regularization, test 추가비용x) 및 단점 존재
1) 비교

- fully connected
- 앞서 말한것
- convolutional
- batch 차원에 대한 평균화 + spatial(공간차원)의 input에 대한 평균화
2) 위치
- FC뒤 or 활성화함수 앞에 위치함
-
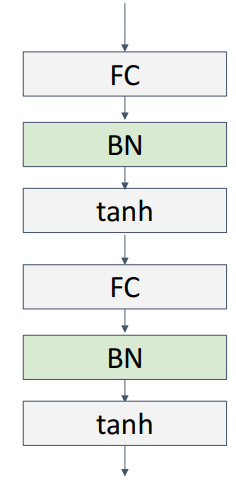
3) 특징
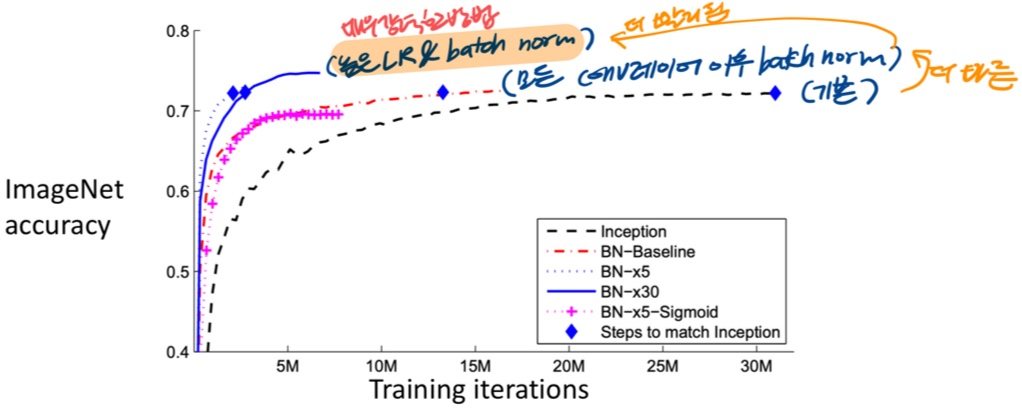
- 장점
- 심층 신경망 train을 더 쉽게 만듦
- 더 높은 LR을 가능하게 하고, 더 빨리 수렴 가능
- 네트워크 초기화에 더 견고해짐
- 학습 중 regularization과 같은 역할
- test시 추가 비용 없음: conv와 병합 가능
- 단점
- 이론적 해석 부족 : 최적화에 도움 되는 이유에 대한 정확한 이해X
- train, test에서 다르게 동작함 → 흔한 버그의 원인이 됨
16. Layer Normalization
📍배치차원평균X, D 평균O
- Batch norm의 train- test에서 다른 작업하는 것에 대한 해결책
- 기존에 대한 변형 → transformer, RNN에서 주로 사용
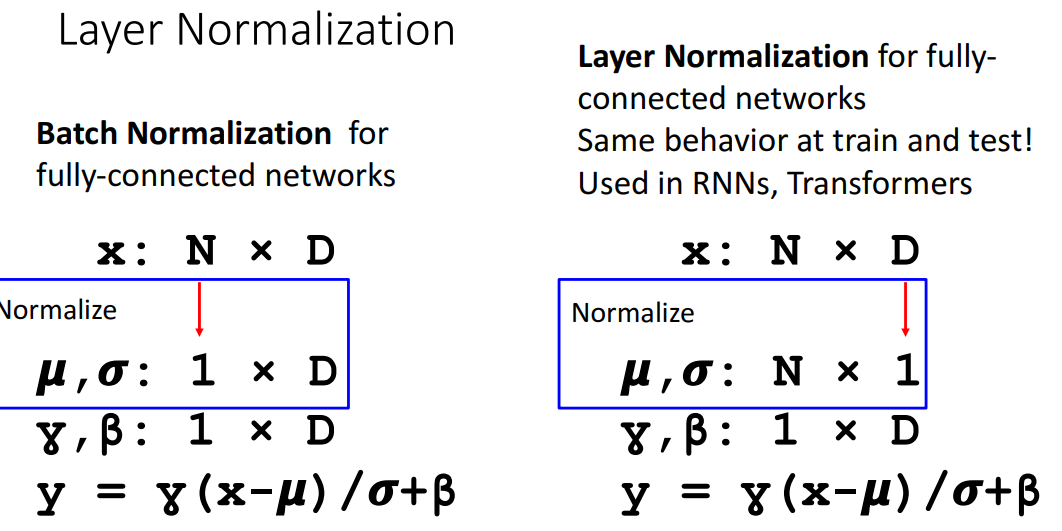
1) 특징
- 기존과 공통점
- $M$, $\sigma$ 구하고 정규화 과정은 똑같음
- 차이점
- 배치차원에 대한 평균 대신, 기능 차원(D)에 대한 평균계산 (↔)
- train 요소에 의존 안하므로, train과 test에 같은 작업 가능
17. Instance Normalization
📍배치차원평균X, D 평균X, 공간차원 평균O
- (CNN에서) 공간 차원에 대해서만 평균 구함

18. 최종 비교
📍CNN에서 Batch norm, Layer norm, Instance norm, Group norm
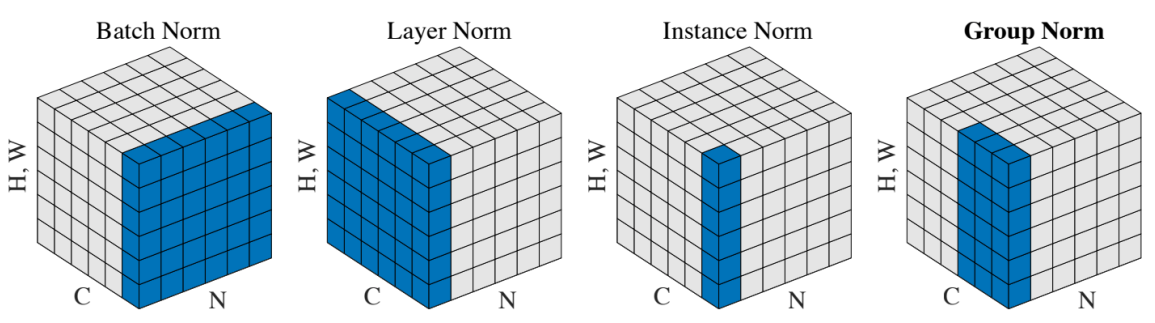
(예를 들어 input이 이미지set (2x3x64x64)가 input이라고 했을 때..)
- Batch norm: 이미지set전부와 각각의 채널별로 정규화한다. (2개의 이미지와 R, 2개의 이미지와 G, 2개의 이미지와 B)(2x1x64x64)
- Layer norm: 하나의 이미지에 대해서 정규화 한다. (1x3x64x64)
- Instance norm: 하나의 이미지에 대해 각각의 채널별로 정규화 한다. (채널 R에 대한 1개의 이미지)(1x1x64x64)
- Group norm: 하나의 이미지에 대해 여러 채널에 대해 정규화 한다. (채널 R과 G에 대한 1개의 이미지)(1x2x64x64)
'2023 딥러닝 > Michigan University DL' 카테고리의 다른 글
| [EECS 498-007 / 598-005] 10강: Training Neural Networks (Part1) (1) | 2024.02.27 |
|---|---|
| [EECS 498-007 / 598-005] 8강: CNN Architecture (1) | 2024.02.27 |
| [EECS 498-007 / 598-005] 6강: Backpropagation (0) | 2024.02.27 |
| [EECS 498-007 / 598-005] 5강: Neural Network (0) | 2024.02.27 |
| [EECS 498-007 / 598-005] 4강: Optimization (1) | 2024.02.27 |