📌 본 내용은 Michigan University의 'Deep Learning for Computer Vision' 강의를 듣고 개인적으로 필기한 내용입니다. 내용에 오류나 피드백이 있으면 말씀해주시면 감사히 반영하겠습니다. (Stanford의 cs231n과 내용이 거의 유사하니 참고하시면 도움 되실 것 같습니다)📌
(📁 아래에 똑같이 제가 정리해놓은 블로그 참고..! 벨로그에 있는게 더 깔끔히 정리 잘되어있습니다)
https://velog.io/@ha_yoonji99/Michigan-Univ-DL-4%EA%B0%95-Optimization
[Michigan DL/cs231n] 4강: Optimization
🔥Michigan University Deep Learning 4강🔥
velog.io
0. 이전시간 + 흐름
- Loss function종류
- cross entropy loss
- SVM loss
- Full loss : regularizaton 더한 loss
- 전체 흐름
- w와 xi, yi로 각각에 대한 점수 내고 → f(xi,w) → 각 class별 loss계산 (이때 regularization으로 과적합 방지)
- 이번 강의 = train data에 맞고, loss 최소화 하는 W값 찾는 방법 구하기!
1. Optimization
1) 개념
- loss function을 최소화하는 W 행렬 찾기
-
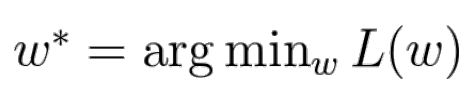
- 해석
- L(w) : loss function
- 저번까지는 이 함수의 내부 초점
- 이번에는 걍 흐름 파악 시 쓰임2) 특징

- optimization의 직관적 생각 (= 매우 큰 고차원 풍경 가로지르기)
- (x,y)point = W
- height = Loss
- 제일 좋은 방법: 정답 알기 →대신→반복적 개선(맨 아래로 이동)
3) Idea
a. Idea#1 : Random Search (매우 별로)
- 방법
-
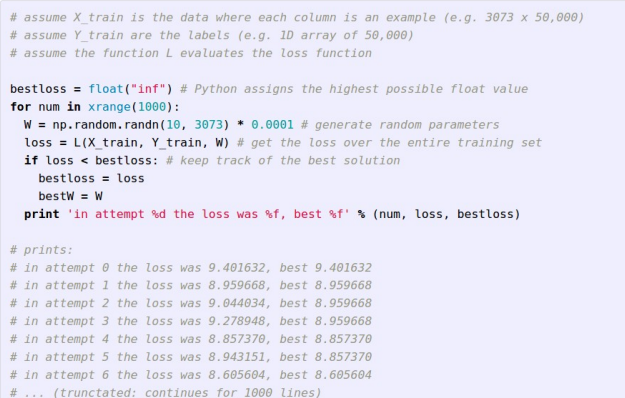
- weight 행렬을 random값으로 생성
→ 각각에 대한 loss구하기
→ 전체 추적
→ 가장 낮은 loss찾기
- 가장 loss가 작은 W로 input과 내적해서 score얻기
→ 얻은 점수들 중 젤 큰애를 predict값으로 설정
→ 정확도 계산(최종 예측 점수)b. Idea#2 : Follow the Slope
- 방법
- 낮은 기울기 따라가기→ 가장 낮은 지점에 도달 할 것
- → 계속 따라가다보면
- 1차원 도함수
-
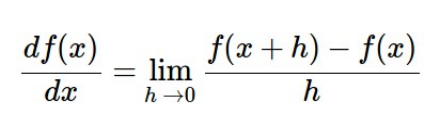
- input & output 모두 single scalar
- 미분 정의 가능
- 어느 지점에서 다 기울기 알수 O
- dL/dw같은 수식으로 전체 loss에 대한 w의 미분값 구하기- 다차원 도함수
- input: vector, output: scalar
- 여기로 가면 내려갈 수 있다는 가장 큰 감소 방향 알수 O
- gradient 크기=경사의 방향 알고리즘
* Numeric Gradient (그냥 기울기 벡터)
ex. 임의의 입력 값에 대한 기울기 어케 계산하는지 확인

- 가중치 행렬의 한 요소를 조금만 변경 → 기울기 알 수 O
= W의 하나의 값을 변화시켰을때, 전체 loss 변함
ex. 위에 대한 예시 -

- 특징
- 위와 같이 하나씩 반복해서 구하는 방법
- 단점
- 매우 느림 (최대 수억개의 data를 train시킨다하면, 매우 비실용적)
- 정확X, 근사치O
* Analytic Gradient (back prop)
- 특징
- (각각 반복하지 않고) 수학적으로 앞서 한 미분 간단히 함
- (벡터 미적학에 따라) W에 대해 정확한 gradient에 대한 수학적 분석 , 표현식 작성 가능
* 두 Gradient 방법 비교 (실제론 둘다 사용)
2. Vanilla Gradient Descent (Full batch)
🔥 Full batch
: 방향이 optimal 함 (full batch여서)
: 기울기 (gradient)활용하여 Loss의 최소를 구하는 알고리즘
: L(w)의 가장 낮은 점에 gradient negative한 방향을 따라가는 알고리즘
(gradient negative라고 표현한 이유: )

1) Vanilla gradient descent
a. 전체 방법 (손실함수 최적화 위한 방법)
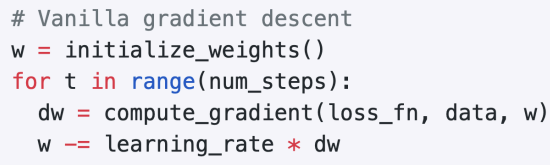
- 가중치 초기화→현재 위치에서 dw(기울기) 계산(-인 이유: 내려가는 방향 찾아야해서(gradient negative))
- → 음의 gradient방향으로 이동하며 w update
- → 일정 반복횟수동안 루프 진행
b. 하이퍼파라미터

(KNN과 달리 실제 조정 많이X, NN에서 좋은 or 나쁜 역할할수도)
- Weight initialization method: random value (매우 중요)
- number of steps (몇번 돌릴건지)
- stopping기준이 여러개 있지만, 딥러닝에선 그냥 고정된 수만큼 반복
- 따라서 예산 or 기다릴수있는 시간에 의해 제약됨
- Learning Rate (=step size)
- 이 gradient를 얼마나 신뢰할 수있는가
- (LR크면) 신뢰많이 하면 → 보폭 크게 대충 확인
- (LR작으면) 신뢰 많이 안하면 → 보폭 작게 세밀하게 확인
- 우리는 최대 감소방향을 얼만큼의 보폭으로 내려가게 할건지 결정
- 너의 network가 얼만큼의 빠르기로 학습할건지
- LR높으면 → 수렴속도 빠름
- LR낮으면 → 수렴속도 느림
- 이 gradient를 얼마나 신뢰할 수있는가
c. 그림으로 이해하기(1) - Direction of greatest decrease of Loss function
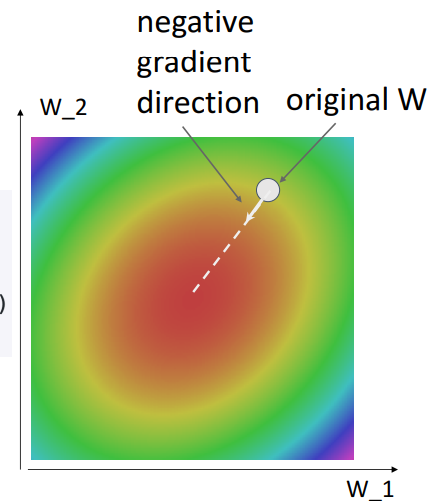
- 해석
- negative gradient계산→ 반복적으로 내리막길 내려감
- → 최대 감소 방향쪽으로 약간의 step size취하고
d. 그림으로 이해하기(2) - taco 모양
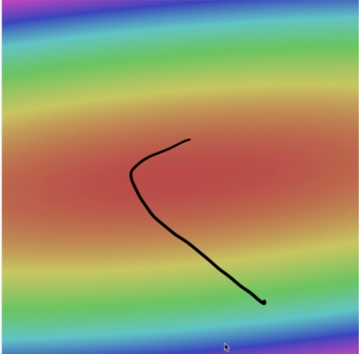
- 해석
- taco 그릇 모양이라 바닥으로 곧장 안감
- 비스듬히 기울여져 있음
- 옆으로 곡선 그리며 그림 아랫쪽으로 돌아옴
- 매우 빠르게 시작
- (dw와 LR곱한 이유)
- gradient 크기 따라 더 큰 LR(step size)취할수도 있음
- 그릇의 바닥에 접근할수록 손실함수 표면 평평해지고, gradient크기 줄어들게 해야돼서
- (그래서 LR을 파라미터화 하는거 → 학습시켜서 변동되게 하려고)
- 알고리즘이 평평한 영역(=손실함수 최솟값)에 접근시 자연스럽게 속도 감소(step size 감소) 되어 LR도 줄어들게 하려고
- (그래서 LR을 파라미터화 하는거 → 학습시켜서 변동되게 하려고)
- taco 그릇 모양이라 바닥으로 곧장 안감
2)(Full) Batch Gradient Descent 수식
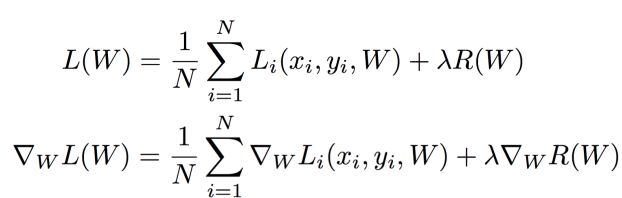
- 해석
- 첫번째 식
- 하나의 example에서 우리 분류기가 얼마나 잘 수행?
- W로 점수 구하고, 확률화해서 L(W)구하기
- 두번째 식
- (Gradient가 선형이여서) gradient는 개별 example의 합
- 모두 sum하면 너무 커져서 계산비용 많아짐
(ex. N=1000만이면, 각각의 Li 전부 구해서 더해야됨)
⇒ N이 엄청 클때 실현가능성 X
—> 해결: Stochastic Gradient Descent (SGD)
- 첫번째 식
3. Stochastic Gradient Descent (Mini batch)
🔥엄청 큰 N에 대해서도 학습 가능해짐_minibatch
1) 개념
- 방향이 optimal 하지 X (full batch아니여서)
- 전체에 대한 작은 sub sample (mini batch)로 손실함수를 근사하고, gradient를 근사함
- 전체 dataset에 대한 loss 계산 대신,전체 배치에서 확률적으로 미니배치 선정
- dataset에서 작은 minibatch를 sampling한걸로 다음 기울기 계산하도록 수정
2) 방법
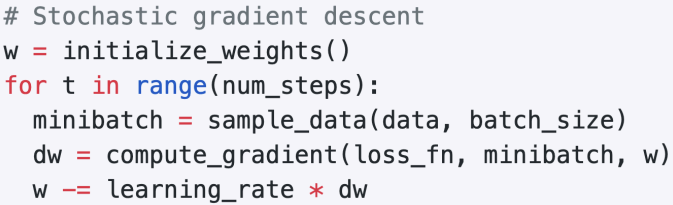
3) 하이퍼파라미터

- 위에 3개 - 기존에 있던거
- Batch size: 각 mini batch에 몇 개의 요소들이 있는가
- 별로 중요X
- (GPU메모리가 감당할만큼) 최대한 크게 만들기 (GPU여러개 & 여러 시스템이면 엄청 크게 batch size해도됨)
- Data Sampling방법
- 이미지 분류에서는 거의 안다룸 (구조화된 예측, 삼중항 일치, 순위 문제 → 여기선 중요할수O)
- 최종 결과에 중요영향X
4) Stochastic인 이유
- Loss function을 확률적으로 보기 때문 (어떻게 확률적으로 보는지?)
-
- 첫번째 식
- 전체 data에 대한 손실 기댓값
- 두번째 식
- sampling으로 기댓값 예측
- N: 모든 data X, batch size
- 데이터 sampling
- 기저확률분포 →(추출)→ data
- 기저확률분포 = 데이터&레이블 결합확률분포
= 데이터가 어떤 분포에서 추출되는지
= 데이터 생성과정 설명
= 실제 데이터 분포X, 확률 모델 가정
- 기저확률분포 = 데이터&레이블 결합확률분포
- 기저확률분포 →(추출)→ data
- 전체 분포에 대해 sample의 작은 몬테카를로 추정 취하여 gradient근사화 가능
-
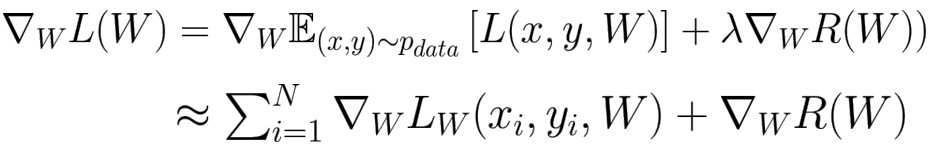
- gradient 근사화
- 전체 확률분포 기댓값을 몬테카를로 방법으로 근사화
- 몬테카를로 방법
= 확률적 방법 사용하여 함수값 추정
= 특정 함수값 구하기 위해 난수 사용하여 sampling
= 함수의 평균값 추정 → 원래 함수값의 근사값으로 사용
⇒ 확률적 접근 → Loss 함수
: 손실함수 계산 위해 몇개 sample이용해서 전체 기댓값 근사화할지 선택5) SGD의 문제점
- Q1) (아래와 같은 상황같이) 한 방향으로 매우 빠르게 변화 or 매우 느리게 변화시, Gradient Descent에 어떠한 문제가 발생하는가?
-
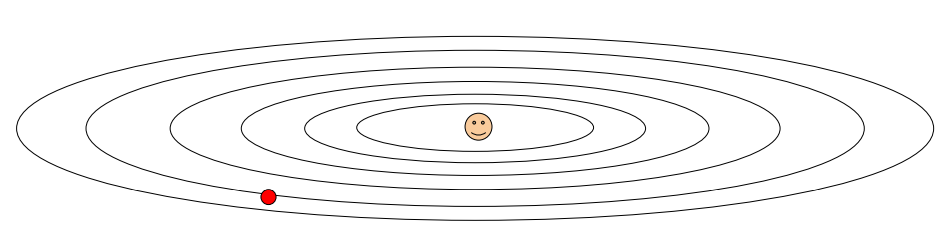
A) (결론) 저차원에서는 매우 느리고, 가파른 방향에서는 불안정하게 진동한다.
- Stepsize가 너무 크면 → step이 진동함
→ gradient계산시, 빠르게 움직이는 차원에서 overshoot할 수 있음
→ overshoot수정하고 다른 방향으로 다시 돌아와야 함
→ 지그재그 패턴 유발
→ 최솟값으로 지그재그 이동하면 수렴속도 낮아짐
- (절충안) stepsize 줄이기 → overshoot 지그재그는 피할수있지만 수렴속도 낮아짐
⇒ (문제점) taco모양처럼 한쪽은 빨리 변하고, 한쪽은 느리게 변하면 stepsize가 크든 작든 어쨌든 문제 발생함(gradient간 차이가 매우 큼)
- (해결책) condition number낮추기 → 헤시안 행렬 조절 or 최적화 알고리즘 조절(=수렴속도 높일수있음)
- (기존 문제점) Loss function은 high condition number을 가지고 있음
= 헤시안 행렬의 (가장 큰 특이값 & 가장 작은 특이값 간 비율이 큼) =high condition number
: 손실함수의 미분값들로 구성된 행렬, 최적화 알고리즘에서 사용
: 헤시안행렬 특이값 = 행렬의 스케일링 정보
= 헤시안 행렬의 스케일링 차이가 큼** (taco모양은 한쪽은 가파르고, 한쪽은 평평)
: 최적화 알고리즘이 Gradient Descent보다 수렴속도 작음
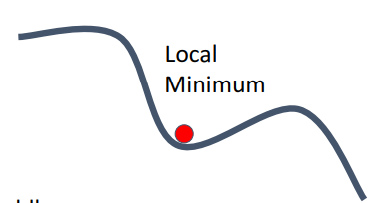
: Gradient Descent가 효율적 작동X → 수렴속도 낮아짐- Q2) loss function이 local minimum or saddle point에 있게 되면 발생되는 문제와 그 해결책?
A) (공통 문제점) zero gradient, gradient descent gets stuck - 고차원일수록 더 자주 발생 (이유: 어떤 한 곳은 증가, 다른 곳은 감소한 부분이 더 많을테니까)- local minimum : 함수 기울기=0이지만, 실제로는 최저점이 아님
- saddle point: 고차원 최적화에서 더 자주 발생, 한방향 증가, 나머지 한 방향 감소
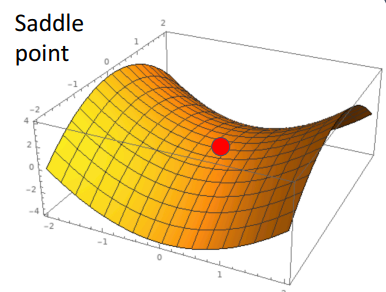
- (안장의 끝 기울기 =0)
- saddle point: 고차원 최적화에서 더 자주 발생, 한방향 증가, 나머지 한 방향 감소
-
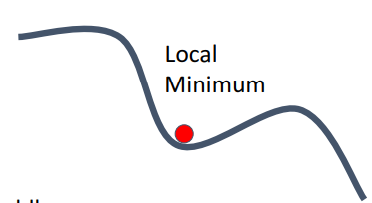
- local minimum : 함수 기울기=0이지만, 실제로는 최저점이 아님
- Q3) 모든 단계에서 update하는데 사용하는 기울기가 가려는 방향으로 곧장 안감(확률적 부분)
A) 명확한 값이 아니고 근사치이기 때문에 잡음이 많을수밖에 없음 → 수렴 시간 오래걸림
4. SGD + Momentum
🔥속도 첨으로 가짐 → local minma, 잡음 극복_v, rho
1) 기존 SGD
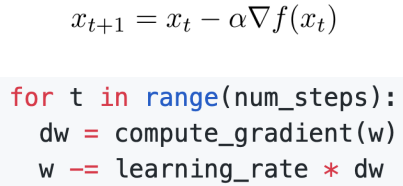
- 해석
- 가중치 초기화 생략(모든 알고리즘 공통 기초라서)
2) 개념
- SGD만 사용했을때의 문제점(진동하는 문제, local minima, saddle point) 극복 위해 Momentum과 함께 사용
- 과거의 방향 기억하여 현재 방향에 반영
- 이전 이동값 고려하여 일정 비율만큼만 다음값 결정 (관성 효과)
- 변수를 가던 방향으로 계속 가게 함
- 같은 방향 이동시, 더 많이 변화 → 학습 속도 빨라짐

- 오른쪽 해석
- dw = w의 gradient계산
- (방향잡기) v(속도)=rho(마찰계수 <1: 과거 속도가 rho로 인해 조금씩 날라감) + dw
- → v(현재속도)에 gradient(dw) 누적되면서, rho로 인해 과거 gradient 잊혀짐
- (그 방향으로 얼만큼 갈지) 현재 방향으로 얼만큼의 보폭으로 갈건지에 따라 w update시킴
3) SGD의 문제점들을 Momentum이 해결한 방법들
a. local minima, saddle point, poor conditioning, gradient noise
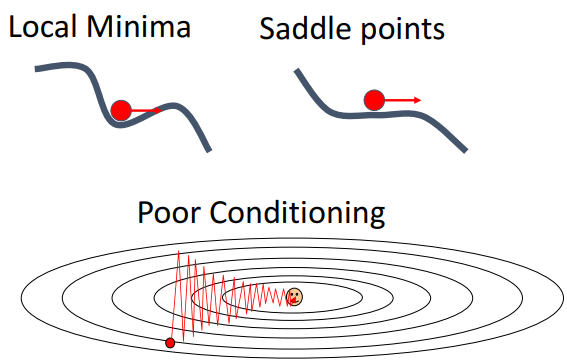
- local minima, saddle point
- v로 인해 속도를 여전히 가져서, local minima에 갇히지 않도록
- poor conditioning
- v가 진동을 매끄럽게 해줌 (기존 방향으로 가도록 해주니까)
- 수평적으로 수렴속도가 가속화될수도 O
-

- gradient noise
- SGD(검) : 모든 지점에서 random noise추가됨
- SGD + Momentum (파)
- 동일 sequence of gradient update
- noise 부드럽게
- 목표에 더 직접적 경로
4) Momentum update (v update)
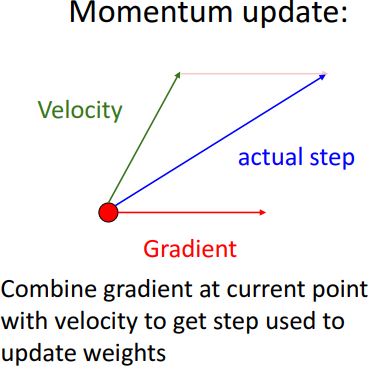
- 개념
- velocity: 방향 제공 ( train에서 gradient와의 과거 평균)
- gradient: 순간 변화율
- 현재 입력값 (빨간점)에서 구한 gradient와 velocity더하여 다음 v(step) 구함
5. Nesterov Momentum
1) 개념
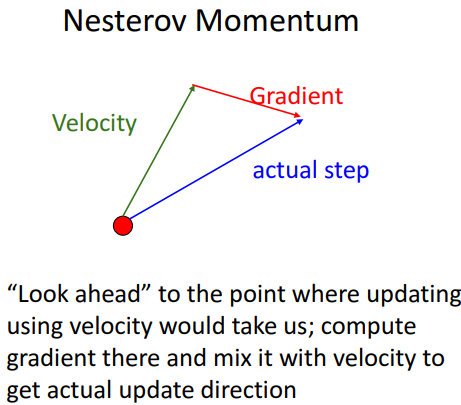
- 기존과 순서만 다름
- 미래를 보고 gradient 방향이 어떨지 계산
- convex function(볼록함수) 성능 good, but 고차원 함수에선 성능 bad
- 현재 입력값에서 velocity만큼 이동 후, gradient구하고 이를 더하여 step 구하기
2) 수학적 표현
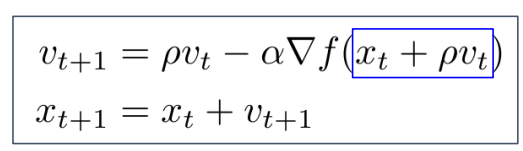
- 해석
- xt + pvt = 현재 입력값 + rho*v
- 미리 기울기 계산
= v방향으로 걸어갈때의 gradient
= 거기서 gradient 계산

3) 그림으로 비교
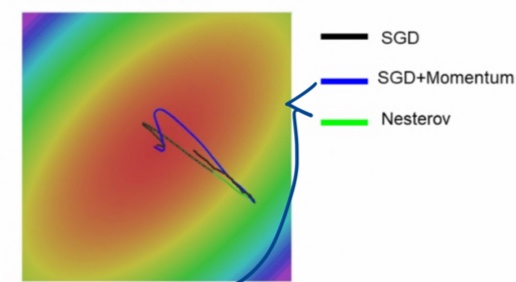
- 공통점
- 시작에서 overshoot하고 다시 돌아옴 (v를 계속 누적함에 따라 큰 속도 얻게됨)
- train process 가속화 (시간 지남에 따라 속도 벡터 구축해서 어케든 빨리 움직이기 가능)
- → 속도 늦추고, 끝을 향해 수렴하도록
6. Adagrad
🔥LR(step) 조절가능_grad_squared
1) 개념
- 각각의 매개변수에 맞게 맞춤형 매개변수 갱신 알고리즘
- adaptive로 학습률(LR, step size) 조정(w업데이트시, w에 적용되는)
- historical sum of gradient values 더하는 대신 gradient 제곱
-
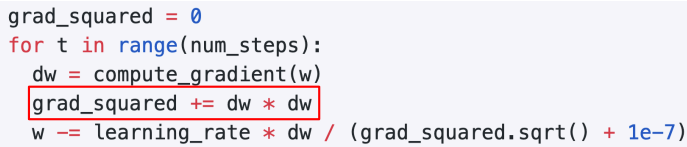
- 1e-7: 분모가 아예 0일때 대비해서
2) 원리
- 상황: 어느 한쪽은 기울기 빨리 변하고(=기울기(dw)가 클때),
→ Adagrad는 큰 값으로 나눠줌 = 분모에 기울기의 제곱만큼 나눠주니, 전체 속도 늦춰짐 - 어느 한쪽은 기울기 천천히 변함(=기울기가 작을때)
→ 작은 값으로 나눠줌 = 분모에 기울기 제곱만큼 나눠주니, 전체 속도 빨라짐
3) 문제점
- grad_squared는 제곱하는거라, 양수만 계속 누적 (=계속 더 큰 숫자로 나누게 됨)
→ grad_squared는 계속 커짐 → step_size감소 = LR 감소
→ 원하는 방향으로 가는 진행 도중에 멈출수O = 바닥에 도달 전 멈출수O
7. RMSProp: Leak Adagrad
🔥LR(step)의 속도 조절까지 가능_decay_rate

1) 개념
- gradient 제곱 값 그대로 누적X, decay_rate 곱함
- step의 속도를 조절 가능 (마찰(decay_rate)추가)
- 마찰(decay_rate)적용시켜서, 속도가 줄어드는 문제 해결
2) 그림으로 비교
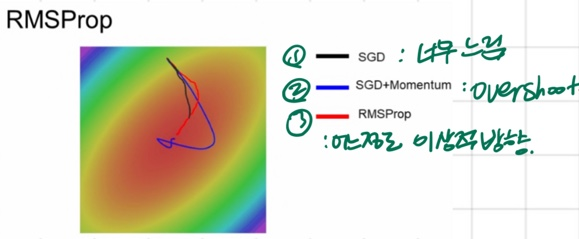
- SGD: 너무 느림
- SGD+Momentum: Overshoot
- RMSProp: 어느정도 이상적 방향
8. Adam: RMSProp + Momentum
🔥적응형 LR + 속도조절
1) 기존에서 가져온 부분
- (Almost) SGD + Momentum 적용 부분 (속도 조절)
-

- **기존 SGD+Momentum**의 **v, rho** → **Adam**의 **moment1, beta1**- (Almost) Adagrad, RMSProp 적용 부분
-

- **기존 RMSProp**의 **grad_squared, decay_rate** → **Adam**의 **moment2, beta2**2) Bias correction
- 발생 가능 문제점
- 최적화 초기에서 발생가능 문제? (beta2 = 0.999)
= moment2 값이 초기에 굉장히 작은 값일수도
→ 이 값이 분모에 있기에, update시 값이 이상하게 튈수도
- 최적화 초기에서 발생가능 문제? (beta2 = 0.999)
- 해결
- bias correction으로 해결하기 (ex. 1e-7)
-

- update시, 현재 step에 맞는 적절한 bias추가하여 값이 초기에 0이 되지 않도록
- 최소한의 파라미터 조정으로 다양한 task수행가능해서 좋음3) 그림으로 이해하기
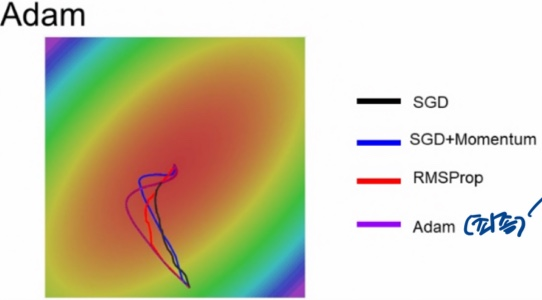
- 결론) 파란선의 overshoot적어지고 ,
빨간선의 적절한 stepsize로 중간에 멈추지 않고 끝까지 최소값 찾기 가능
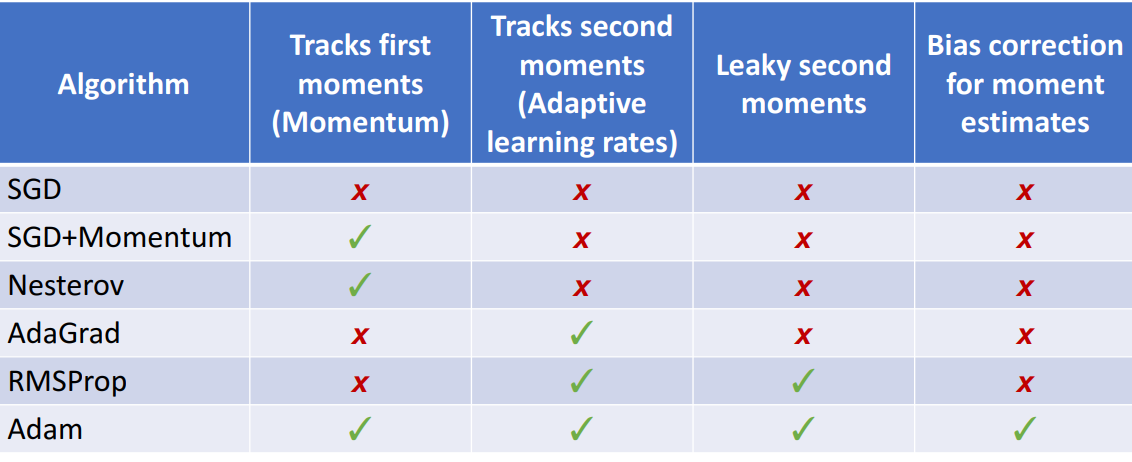
9. 최종 비교
'2023 딥러닝 > Michigan University DL' 카테고리의 다른 글
| [EECS 498-007 / 598-005] 8강: CNN Architecture (1) | 2024.02.27 |
|---|---|
| [EECS 498-007 / 598-005] 7강: Convolutional Neural Network (0) | 2024.02.27 |
| [EECS 498-007 / 598-005] 6강: Backpropagation (0) | 2024.02.27 |
| [EECS 498-007 / 598-005] 5강: Neural Network (0) | 2024.02.27 |
| [EECS 498-007 / 598-005] 3강: Linear Classifier (2) | 2024.02.27 |