📌 본 내용은 Michigan University의 'Deep Learning for Computer Vision' 강의를 듣고 개인적으로 필기한 내용입니다. 내용에 오류나 피드백이 있으면 말씀해주시면 감사히 반영하겠습니다. (Stanford의 cs231n과 내용이 거의 유사하니 참고하시면 도움 되실 것 같습니다)📌
(📁 아래에 똑같이 제가 정리해놓은 블로그 참고..! 벨로그에 있는게 더 깔끔히 정리 잘되어있습니다)
https://velog.io/@ha_yoonji99/3%EA%B0%95-Linear-Classifier
[Michigan DL/cs231n] 3강: Linear Classifier
🔥Michigan University Deep Learning 3강🔥
velog.io
1. Parametric Approach
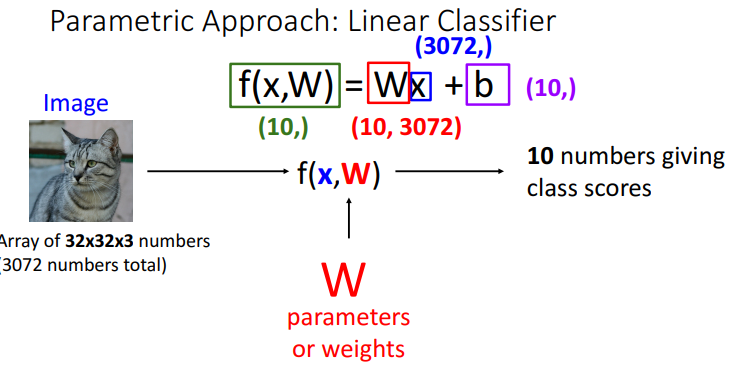
1) input image : 32x32x3 픽셀의 이미지
2) f(x,W) = 선형 분류기 (가장 단순한 분류기, Neural Network의 기본)
- x = input 이미지 픽셀 벡터(32x32x3=3072)
- 벡터로 하는 이유: input data는 모두 차원, 크기 다를수 O → 각기 다른 공간구조 파괴(입력 데이터 재구성)하여 통일되게 input하려고
- W = 가중치
- f(x,W) = Wx (기본)
- b = bias (추가적인 가중치 역할)
- 사용 이유: bias 없으면 무조건 원점 지나는 한계 극복, 비선형으로 만들어서 더 분류 잘하게 하려고
3) 10 numbers giving class scores
- 각 class(category) 10개 별로 점수매김
4) 예시
- step1) input image 벡터화
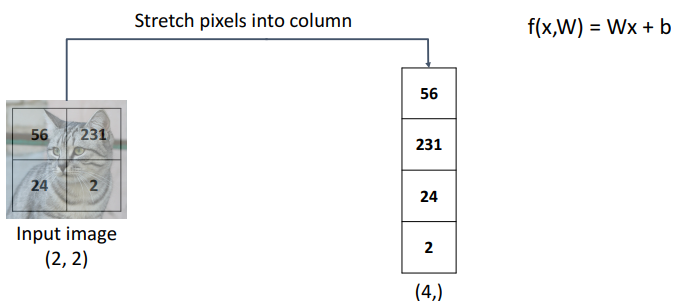
- step2) 가중치 적용 + bias 적용
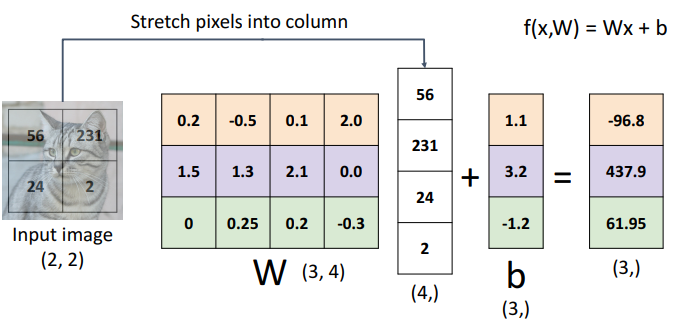
- b(3,) → 3: 정답 category 수
- W(3,4) → 3: 정답 category 수, 4: input 차원 수
2. 선형 분류의 여러 관점들을 통한 특징
: 선형 분류 = 행렬, 벡터 곱셈의 간단한 모델
: 여러 관점들로 선형 분류의 특징들을 확인해보자.
1) 대수(수학)적 관점 (Algebraic viewpoint)
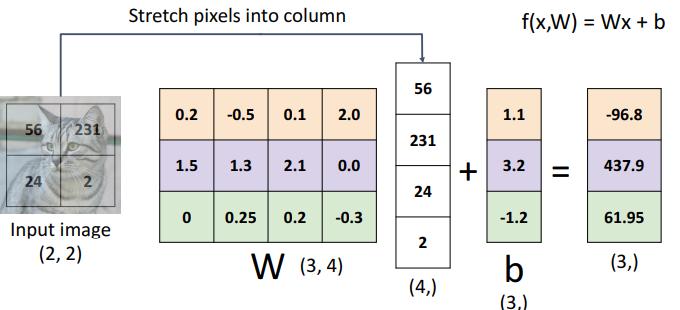
a. 개념
- 위의 예시와 같이 행렬 내적 + 벡터화
- input data를 벡터화하는 방법
- 수학적 관점에서 행렬 내적 계산
b. 특징
- 예측이 선형임
- ex. bias가 없다고 생각하고 f(x,W)보면
- 상수 c에 따라 예측점수 달라질수도(선형이라 가능한거)
- 0.5 * image = 모든 픽셀 채도 감소
- 예측 점수도 모든 카테고리에 대해 1/2 되는것 (선형이라서)
- 직관적X(예측 점수가 변경돼서 상수 c곱하는건 직관X)
- 상수 c에 따라 예측점수 달라질수도(선형이라 가능한거)
- ex. bias가 없다고 생각하고 f(x,W)보면
c. cf) Bias Trick (잘 사용X)
- 개념
- 가중치 행렬에 bias 벡터 통합시키기
- 통합시켜도 분리해서 계산하는 것과 동일 결과 도출
- input data가 기본 벡터 가질때 사용됨
- 이 개념보다, 그냥 대수적 관점의 선형 분류기가 더 사용 多
- 예시
-
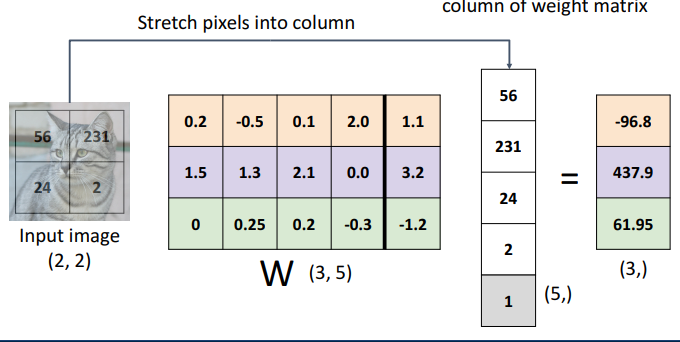
- W(3,5): 3개의 정답 카테고리, 5개의 vector크기 (한줄 늘어나서)
- (5,) : 가중치 열이 1개 더 늘어나서 걍 의미없이 1 붙이는 것- 단점
- 가중치와 bias를 별도 매개변수로 분리하여 처리하는 경우 많음
- (ex. 초기화, 정규화)
2) 시각적 관점 (visual viewpoint)
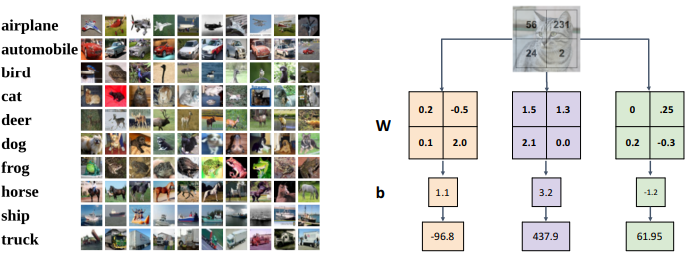
a. 개념
- Weight을 input과 같은 모양으로 재구성
- bias를 각각의 weight에 붙이기(원래는 한 줄의 벡터로 만들었음)
- 좀 더 직관적으로 이해가능
b. 특징
- 각 정답 카테고리별로 하나의 template 존재 (template matching)
-

- 명확한 분류가 어려울 수 있음
- 이미지의 context 단서에 강하게 의존
= 배경색에 따라 높은 점수 얻을 수 있기에 명확한 분류 어려움 = 뱅기, 개, 사슴 같은 물체 category 인식하고 싶으나, 실제로는 input image의 더 많은 증거 사용 (개체 자체보다)- ex1. plane template (일반적으로 파란 이미지)
- (이 가중치 매트릭스 사용하는 경우) 파란색이 많은 input image는 plane class에 대한 높은 점수 받을 것
- ex2. car template
- cifar10에는 red car이 많은걸 알수 있음 (녹색, 파란 car 인식X)
- input image에 대한 다양한 변수(색, 방향) 인식 X
- cifar10에는 red car이 많은걸 알수 있음 (녹색, 파란 car 인식X)
- ex. 다른 방향 보는 말에 대한 template을 별도 학습 불가 (two head로 나옴)
3) 기하학적 관점 (Geometric viewpoint)
a. single pixel
- 앞에서 했던 것과 동일
- 임의의 픽셀을 하나 가지고 score 경계 만드는 것
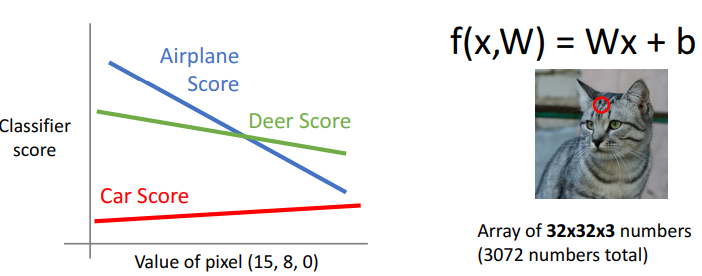
- 해석
- value of pixel(15,8,0): 개별값 변경에 따른 픽셀값 변화
- classifier score: 이 픽셀에 따른 category들의 경계선
b. multiple pixel
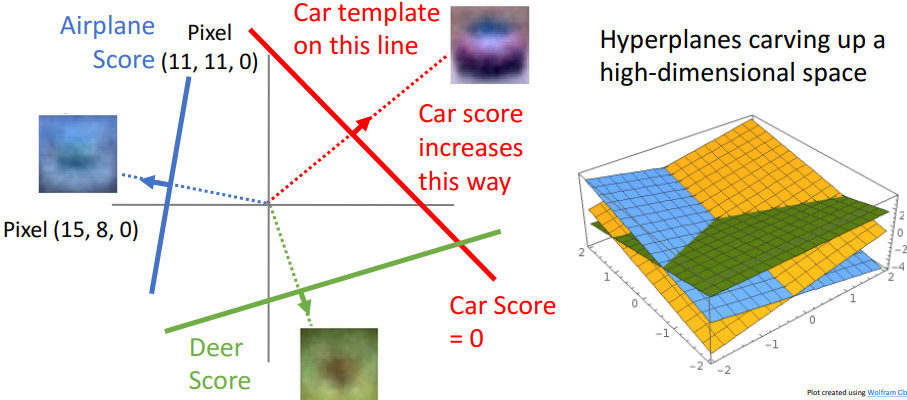
- 특징
- 일차식을 초평면으로 표현하여 3차원에 위치시킴
- 고차원 유클리디안 space 요구
- 매우 높은 차원의 공간으로 이미지 전체 공간 취함
- category 1개당 1개의 초평면
- W(가중치 값)=각 선분의 기울기 (걍 기존 1차식을 3차원 한거니까)
- 장점
- 선형 분류기가 어떤 category를 인식 가능한지 파악 가능
- 단점
- 기하학이 어떻게 작용하는지에 대한 물리적 직관 알기 어려움 (우리의 직관은 저차원에 익숙해서)
- c. 선형분류가 잘 안되는 경우 (기하학적 관점에서) → 걍 분류에 한계있음 이정도*
-
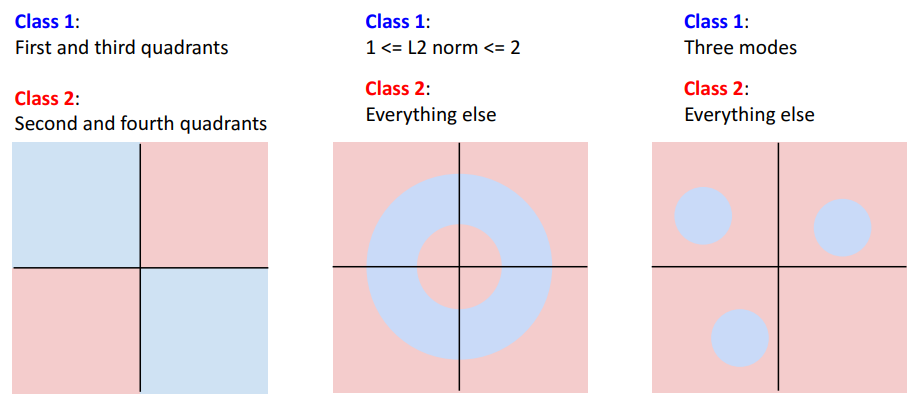
- 첫번째 예시
- 서로 다른 카테고리에 속할때
- 두번째 예시
- 연속적이지 않을때
- 세번째 예시
- 다른 mode들 가질때 (ex. 말이 다른 방향 봄)
고차원 픽셀 공간에서 오른쪽 보는 말에 해당하는 공간의 일부영역이 있고, 다른 방향을 보는 말에 해당하는 완전 분리된 공간 영역 있음
- 다른 mode들 가질때 (ex. 말이 다른 방향 봄)
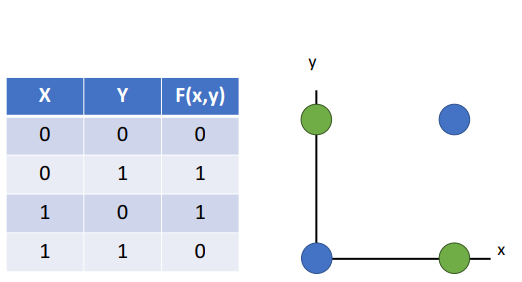
- 퍼셉트론
- 특징
- 최초의 기계학습 알고리즘
- 이진 분류 시 사용
- 입력값+가중치>임계값 = 1 , 반대면 0
- 단층 퍼셉트론: 1개의 출력뉴런, 선형 분류에만
- ex. 퍼셉트론이 XOR함수 인식할 방법X
- (= 하나의 선으로 파란색, 초록색 영역 분류X)
- 다층 퍼셉트론: 여러 은닉층, 비선형 분류도 가능
- 특징
3. Score함수 작동 원리 파악 중요성
1) 필요성
- 선형 분류기가 있으므로 , score예측 가능
2) 앞으로 알아야 될 것
- Loss function: 최적의 W업데이트 위해서
- Optimization: train data활용하여 가능한 W모두 검색하고, 우리 데이터에 적합한 W찾기
4. Loss function
1) 개념
- 분류기가 데이터에 대해 얼마나 잘 수행하는가
- 언제, 어떤 유형의 모델이 좋은지 알려줌
- loss 작음 = good classifier
- loss 큼 = bad classifier
- = objective function, cost function
- cf) Negative loss function
- 점수가 높을수록 → good classifier
2) 구현 식
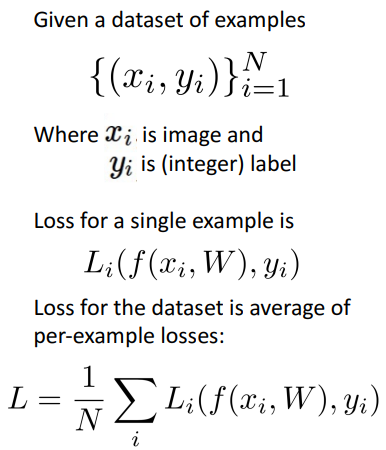
a. 첫번째 식
- xi = input image
- yi = 정답 카테고리 (ex. cat)
b. 두번째 식
- f(xi, W) = input에 가중치 적용한 함수
- yi = 정답 카테고리
- 전체 = 예측값과 실제값 사이의 badness측정
c. 세번째 식
- N = data 총 개수
⇒ 각기 다른 task마다 각기 다른 유형의 loss function 써야됨
⇒ 하나의 task에서도 다양한 유형의 loss function이 있는데, loss function에 따라 손실 정도가 달라짐 (5번. Multiclass SVM Loss가 그 예시)
5. Multiclass SVM Loss
1) 개념
- 정답에 높은 점수, 오답에 낮은 점수
2) 시각화 그래프
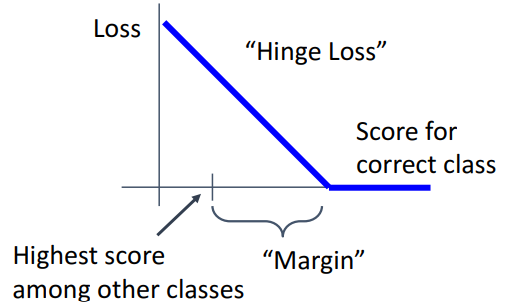
a. margin
- 사용 이유
- loss낮춰서 과적합 낮추고, 일반화 높임
(margin없으면 그냥 무조건 틀렸다고 해버려서 loss가 더 높아짐)
- loss낮춰서 과적합 낮추고, 일반화 높임
b. 전체 해석
- 정답과 오답의 category score비교
- 선형적 감소
- 정답 > 오답+margin
- hinge loss라고 불림
c. 수식 (그래프를 식으로 표현)

- 첫번째 식
- xi=input image
- yi=정답 카테고리
- 두번째 식
- linear classification 결과
- 세번째 식
- 정답 class ≥ 오답 class+1 ⇒ loss=0
- 나머지 ⇒ 선형
3) 예시 계산

- 전체 loss값 = 모든 loss합 / 카테고리 개수
4) Multiclass SVM Loss Question
- Q. car(옳게 분류된 경우)의 이미지 점수가 조금 바뀌면 전체 loss가 어떻게 되는가?
A. 여전히 손실 =0- 올바르게 분류 되면, 예측점수가 약간 달라져도 손실에 큰 영향X
- 정답과 오답의 차이가 margin보다 크면 정답
- Q. loss값의 가능한 min, max값은?
A. min =0 ; 정답점수가 오답점수보다 높을때 max = 무한대; 정답점수가 오답점수보다 훨 낮을때- Q. 모든 점수가 random일때, loss가 어떻게 되는가?
A. 총 Loss값 = c-1이 됨.
가중치 행렬이 random으로 초기화되면, 예측점수도 각 카테고리별로 random일것- ex. 모두 small random value일때, 모든 score(오답, 정답)이 거의 비슷하거나 오차가 0에 가까운 경우
→ 하나에 대해 Loss 값 = small value - small value + 1(margin)
⇒ 총 c-1 개 있으니, Loss값은 c-1이 되는것- Loss값 > c-1이면, 랜덤보다 못한 성능인것 (랜덤으로 넣은것보다 손실이 크니까)
- 모든 점수 랜덤일때, 예상한 것과 다른 손실 발생시 버그 확률 높아짐
- 새 손실함수 구현 및 학습 (⇒ 작은 난수값으로 어떤 종류 손실쓸건지 예상)
- ex. 모두 small random value일때, 모든 score(오답, 정답)이 거의 비슷하거나 오차가 0에 가까운 경우
- Q. 모든 class에 대해 sum이 적용된다면? (정답값을 포함해서 Loss구하기)= 분류기에 대해 동일 선호도 나타냄
- = 모든 손실은 1의 값으로 부풀려지지만, 상대적 할당이 있기에 순서 변경X
- A. 모든 손실에 +1 (max(0,1)=1) 하는 것
- Q. sum대신 평균 내서 손실 구한다면?
A. 가중치 matrix = 기존과 동일
loss 값 = 기존보다 작아짐 (평균내서)
= (모든 Loss) * (c-1)이 되는 것 (왜인진 모르겠음) -

- Q. 제곱을 취한다면?
A. 비선형 방식으로 loss function of weight이 선호도를 엄청 바꿀것 - Q. 총 Loss값을 구할때, L=0이라면 그렇게 만드는 W가 유일한가?
A. No, 2W도 L=0이 될 수 있다.= 여전히 margin 초과 ⇒ Loss =0
⇒ 그렇다면 동일 손실 2가지 W, 2W중에 뭘 선택?
—> Regularization으로 해결 - = 분류기가 선형이기에, 모든 예측점수도 2배가 됨
6. Regularization
1) 개념
- 잘 수행되는 훈련 데이터에 맞서싸우는 목적함수 or 전체 학습 목표에 추가
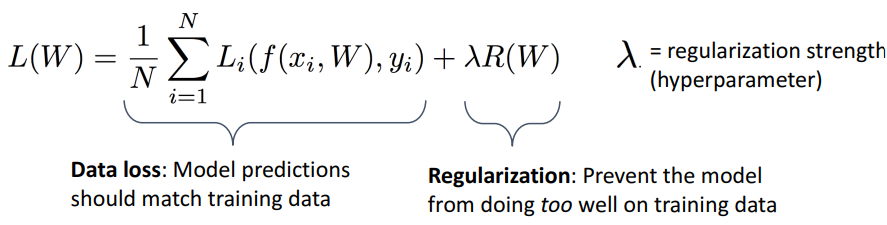
- Data loss = 기존 loss = average loss
- 얼마나 train data 잘 예측하는지
- Regularization
- train data에 포함 X
- train data에서 과적합 방지, 모델에 시도하는 것 외에 다른 작업 제공
- Regularization Strength
- 모델이 얼마나 잘 예측하는지 절충점 제어
- strength 높으면 → 과적합 감소 (틀린 값을 좀 봐줌)
2) 예시
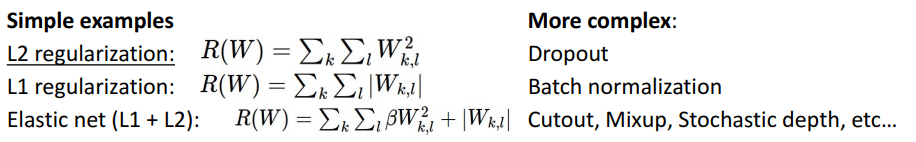
3) 사용 목적
- 훈련 error를 최소화하는 작업에서 인간의 주관 개입 ok
- 과적합 피하기 → 일반화 더 잘하기
- 곡률 추가하면서 최적화 더 잘하기
4) 특징
- (W에 대해) 선호도 표출 (앞에서 W or 2W 뭘고를지 해결)
- loss함수 + (L1, L2)정규화 추가하면 추가적인 선호도 표현가능
- = W1, W2중 우리가 선호하는게 뭔지 모델에 알릴수O
- ex. L2 regularization이 w1선호? w2선호?
-

- 해석
- w1에 L2적용 → 1
w2에 L2적용 → 1/4
=⇒ L2는 Loss가 더 낮은 w2를 선호한다는걸 알 수 있음- 과적합 방지
-
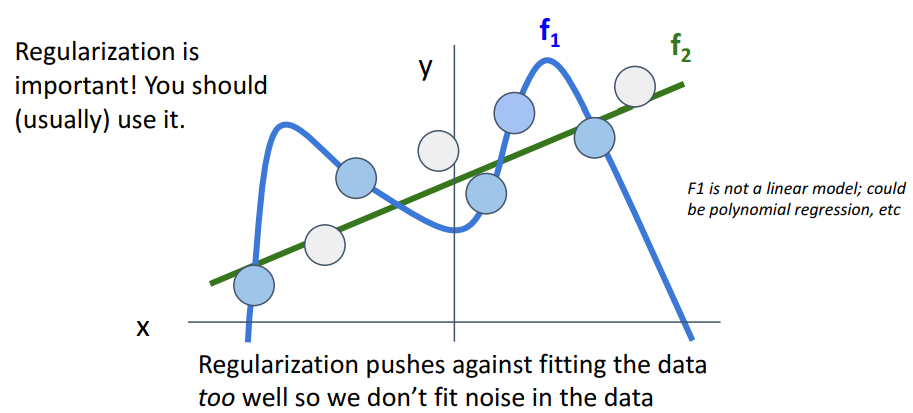
- 해석
- f1: train data를 완벽히 커버하지만, 보이지 않는 data에 대해선 성능 떨어짐
- f2: 선형이라 더 simple 하지만, 보이지 않는 data에 대해 성능 높음7. Cross entropy Loss
1) 개념
- SVM Loss보다 신경망 학습시 더 일반적으로 사용
- SVM Loss : 예측된 점수에 대한 해석 제공X, 걍 대소비교(정답점수>오답점수만) 가능
- Cross entropy Loss: 예측 점수에 대한 확률적 해석 제공O
2) 적용 방법
- Step1: classifier에 의해 raw score 나옴
- step2: 지수함수화(exp)
- 모든 결과값들이 0이상(음수X)
- step3: 정규화 (normalize) → softmax로
- 정규화 후 확률 더하면 1
- softmax 사용 이유
- max함수에 대한 미분가능한 근사여서
- 미분가능하기 원할때 사용(미분가능해야 학습 가능하여 W update함)
- 전체 중의 비중 확인 가능
- step4: Loss계산
- log쓰는 이유: 대소관계 안변해서
- log앞에 - 붙이는 이유: 최대 우도 추정 인스턴스여서
- : log취하면 숫자가 클수록 작아짐, 근데 loss는 숫자가 클수록 커지고 작을수록 작아져야 해서 -곱함 (손실이 작아져야 되니까 = GD가 작아져야돼서)
- step5: 정답 확률과의 비교
- 공식1: KL Divergence
3) Question
- Q. Cross entropy Loss에서 min, max는?
A. min=0 → target분포가 0과 1일때, 예측과 타겟 분포가 떨어져있을때 가능 - max=무한대
- Q. 모든 점수들이 작은 random일때, Loss는?
A. -log(c)- 균일한 점수분포 예측 → softmax → 예측확률분포가 c개 category에 대해 균일 (각각 1/c인것) → -log(c)
'2023 딥러닝 > Michigan University DL' 카테고리의 다른 글
| [EECS 498-007 / 598-005] 8강: CNN Architecture (1) | 2024.02.27 |
|---|---|
| [EECS 498-007 / 598-005] 7강: Convolutional Neural Network (0) | 2024.02.27 |
| [EECS 498-007 / 598-005] 6강: Backpropagation (0) | 2024.02.27 |
| [EECS 498-007 / 598-005] 5강: Neural Network (0) | 2024.02.27 |
| [EECS 498-007 / 598-005] 4강: Optimization (1) | 2024.02.27 |