1. Introduction
- SIV(희소하지만 정보를 제공)의 효과적 활용 위해, 이 논문의 독자적인 접근방식이 rMSE면에서 기준선 접근방식보다 뛰어남
- SIV가 손상되면 논문의 독자적 접근방식도 성능 낮아질것
- 결론*) 논문의 접근방식은 예측에서 SIV를 더 효과적 사용가능
내재+외재 = 예측정확도 향상
But 혈당과 같은 생리학적 변수의 예측에서는 내재+외재에서 예측 정확도가 향상되는 경우 없을수있음
- 보조신호와 대상 신호간의 비제로값이 상대적 불일치 때문
- 보조신호(외재)가 대상 신호(내재)에 영향 미치는데 매우 희소( 희소하지만 정보를 제공하는 변수(SIV)
=⇒ 희소성에도 불구하고 SIV를 활용하여 전반적인 예측 개선
SIV문제
- 언제 발생) 부가변수가 시간에 따라 대상 변수의 크기를 증가시키거나 감소시킨다는 것을 알고는 있지만 정확한 효과가 알려지지 않을 때 발생
- 왜 문제점인가) 일반적인 다중 입력 예측 접근방식이 부가변수 활용 못하도록함.(=단일 입력만 처리 가능)
SIV문제 극복 모델
- 예측정확도 향상되는 방향으로 활용
- 중요한 변수가 대부분의 시간에서 0값을 가질때 발생하지 않도록
The Linked Encoder/Decoder
- 내재적 효과와 외재적 효과의 분리(연결된 2개의 디코더 네트워크통해 구현) + 도메인 지식의 통합(SIV네트워크의 출력 제한)
Contribution
- 희소하지만 정보를 제공하는 변수(SIV) 문제를 제시합니다.
- SIV의 효과를 분리하고 도메인 지식을 통합함으로써 SIV를 활용하는 혁신적인 예측 접근 방식을 제안합니다.
- 혈당 측정을 예측하는 문맥에서 모델을 평가하고, noise가 적은 경우에도 SIV를 효과적으로 활용함을 보여줍니다.
2. Problem Setup
다중 입력 단일 출력 시계열 예측작업
- 기존엔 단일 대상변수의 미래값 예측
- but 추가 보조변수(x’)의 미래값 예측 하도록
하려는 것
- 대상신호의 다음 h개의 시간점 예측
걍 SIV문제를 혈당예측(BG농도 추정)에 활용하겠다.
- 인슐린, 탄수화물 측정 이후 정확한 예측 중요해서, 그 시간동안 가장 혈당 변동성이 크고 개인에게 위험 제공해서
3. Methods
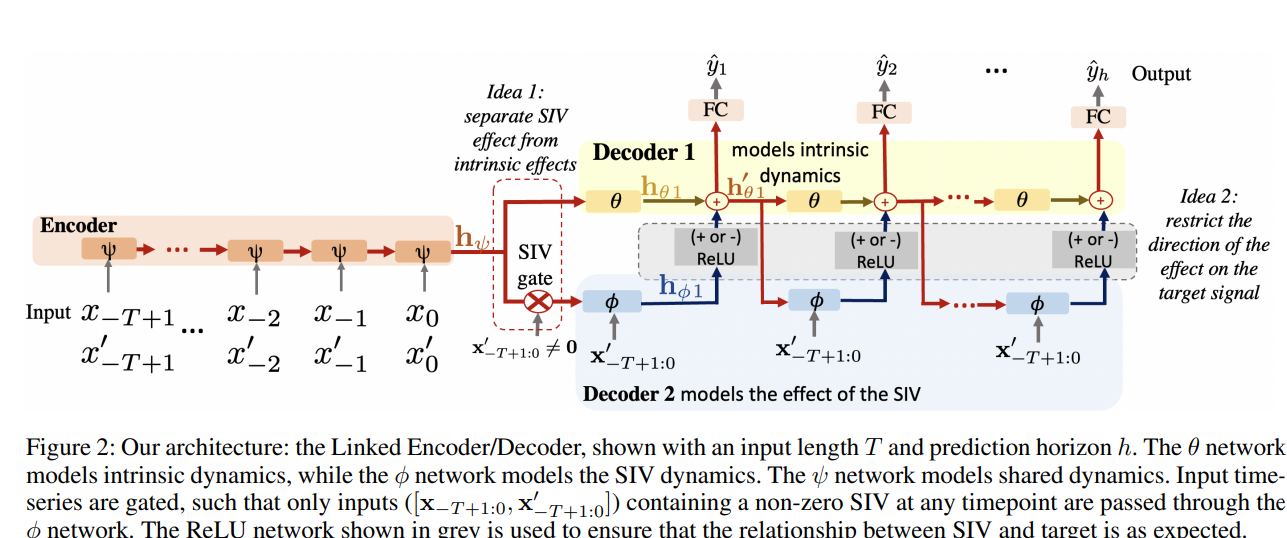
- 인코더 1개 , 디코더 2개(SIV동태, 내재적 동태)로 구성
특징
- 디코더 공통: hidden state공유하며 병렬처리
- SIV 디코더: SIV신호를 입력받음
$h_0θt$는 두개의 디코더의 합
- 내재, 외재적 효과 모두 포착
- 즉, yˆt = FC($h_0θt$)
주의점
x0=0일때는 φ가 활성화되지 않으며, h0θt = hθt가 됨
SIV신호: 시간별로 이동되어, 인코더의 상대적 위치를 암묵적 표현
하나의 SIV를 가진 설정에 대한 제안된 아키텍처 개요 제시
여러 SIV가 있는 경우, 보조 디코더 수 늘리고, 각 SIV의 알려진 효과에 따라 제한 적용
φ
관련된 SIV신호와 $h_0θt$만 입력받음
$h_0θt$
모든 SIV디코더 시스템에의해 수정됨
FC 이후의 디코더 단계에 전달되는 hidden state
- SIV 개수 +1개
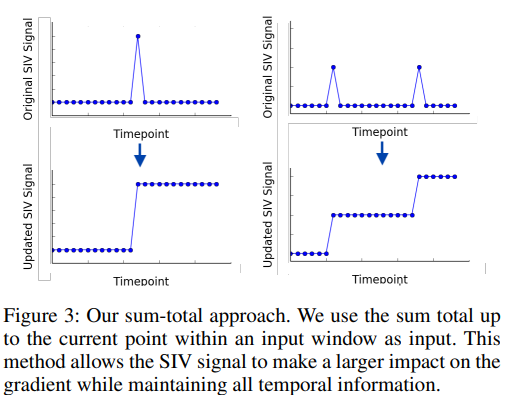
SIV 활용이 어려운 이유
- SIV가 입력 창의 단 하나의 시간점에서만 발생
- 훈련 중 gradient에 거의 영향X
Figure3
- 기준선, 제거 실험에 대해 성능 향상
- 입력시계열의 첫번째 0이 아닌 SIV값 이전까지의 값=0
- 계속 누적되어 구성됨
4. Experimental Setup
<예측>
- BG: 혈당
- 목표: 2가지 SIV (탄수화물, 인슐린 볼러스)기반하여 미래 30분 후의 BG(h=6)예측
- h=6: 일반적인 BG 예측 벤치마크
- 대상, 보조변수: 0~1사이 스케일링 , 최대 예상값에 선형스케일링 적용
- 각 개인 훈련, 검증, test data: 겹치는 길이 T + h (모델 입력과 레이블로 사용)
<평가>
- SIV가 제거될때, 모델이 학습할 수 있는 대상변수로부터 최대 정보량 학습할 수 있도록
- SIV가 없는 데이터에서 훈련 및 테스트
- 기준 인코더/디코더 오차와 SIV사용의 개인별 개선도 비교
- 이 방법이 기준에 비해 개인별로 얼마나 큰 개선 제공하는지 확인
- 기준에서 SIV 잘 모델링X → 개인에 대해 기준오차 높음
- SIV 사용 낮으면 → 우리 접근방식이 기준에 비해 더 큰 개선 제공
5. Conclusion
- SIV(Silent Information Versioning) 문제는 RNN을 사용한 다중 입력 예측에서 발생하는 일반화 성능 저하 문제입니다.
- 이 문제는 희소하게 샘플링된 변수(SSV) 문제와는 별개로, 결측치와 노이즈를 처리하는 기존의 보간 접근 방식으로는 해결할 수 없습니다.
- SIV 문제는 아직 해결되지 않았지만, 변수 간 상호 관계를 학습하기 위해 어텐션 메커니즘과 같은 여러 기법이 제안되었습니다.
- 그러나 이러한 기법들은 희소성 문제를 고려하지 않거나 도메인 지식을 충분히 활용하지 않는 경우가 많습니다.
- SIV 문제를 해결하기 위해 변수 간 관계를 명시적으로 모델링하는 다양한 접근 방식이 제안되었지만, 희소성 문제를 다루지 않거나 도메인 지식을 충분히 활용하지 못한 경우가 있습니다.
- 우리의 연구는 SIV 문제를 해결하기 위해 은닉 상태의 부호를 제한함으로써 더 유연한 접근 방식을 제안하고 있습니다.