0. Abstract
- LTSF해결위한 Transformer based 해결책의 급증
- Transformer는 의미론적인 상관관계를 잘 해결함
- 순서가 있는 연속적인 point에서 시간적 관계추출해야됨
- Transformer에서 encoding, token이용하면서 정보를 순서대로 놓아도,
- self attention매커니즘의 순서가 변하지 않는 것은 일시적 정보손실을 반드시 낳는다*
- LTSF-Linear가 기존의 정교한 Transformer-based LTSF 를 넘어서 좋은 성능 보여줌
1. Introduction
시계열
- 시계열 문제는 data기반 세계에 만연함
- 시계열 문제 해결 변천사 : 머신러닝 → 딥러닝
Transformer
- Transformer 장점: 순서기반 모델, 병렬적이지 않은 해결, 다양한 적용 분야(NLP, 음성인식, cv
- 최근 시계열 위한 Transformer기반 해결책 엄청 많이 나옴
- 흔하지 않은 LTSF 해결위한 transformer모델들
Transformer 원리
- Transformer원리: multi-head-self-attention 매커니즘→ self attention이 긴 시계열에서는 잘 작용못함
⇒ 요약: 긴 시계열 예측에서 Transformer가 self attention문제로 정보손실 발생할수도있는데, 진짜 효과적인거 맞냐? (목적: 긴 시계열 예측(LTSF))
non-Transformer로의 LTSF해결
⇒ 요약: 우리는 transformer based말고, non-transformer based인 DMS예측으로 해결하겠다
LTSF-Linear 소개
- LTSF-Linear 개념: 1layer 선형 모델로 과거 시계열 회귀하여 미래 바로 예측함
- LTSF-Linear 적용: 9개의 널리쓰이는 dataset들에 적용해봄
- LTSF-Linear 적용결과: 현존하는 복잡한 Transformer보다 20~50% 더 성능 좋음
2. Preliminaries: TSF Problem Formulation
수식 해석
- X: 과거 시계열을 나타내는 변수
- C: 여러 시간 단계에서 C 변수의 값
- L: 현재 시점에서 모델이 과거 데이터를 얼마나 멀리까지 살펴볼 것인지를 지정하는 값
- Xti: time step
X집합 = t=1부터 L까지의 시간 집합들
T: 미래 time step
측정한 과거시점(L)+1 ~ L+T
= 현재2023년 ~ 2021년(L), T=5이면,
X^은 2022년(L+1) ~ 2026년(L+T)
⇒ 요약: DMS가 긴 시계열에 유리하다.
3. Transformer-Based LTSF Solutions
Transformer-based models로 LTSF에서 많이 발전함
vanilla Transformer model의 문제점과 여러 해결법들
(vanilla Transformer model로 LTSF문제 다룰때의 문제점:
기존 self attention으로는 2차 시간/기억의 복잡성(앞에껄 기억못함)문제 발생
& 자동회귀 decoder로 인해 error누적)
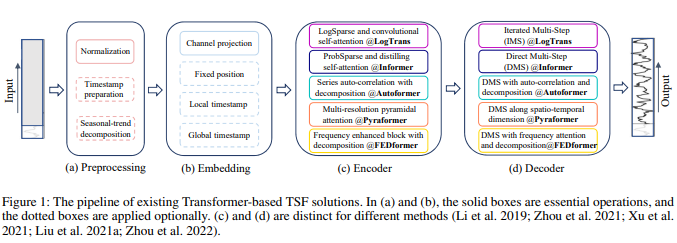
(a) preprocessing: 시계열 데이터를 구성 요소로 분해 : 전체적인 추세, 계절성 패턴, 주기적인 변동 및 잔차 오차
→ 분해해서 예측, 이상치 탐지, 시뮬레이션 등에서 활용가능
(b) embedding: 긴 시계열의 의존성 포착 및 시간적 문맥 강화
(c) encoding: 긴 시계열의 의미론적 유지를 위한 2가지 전략
(d) decoding
*Transformer based LTSF solution들은 self attention의 순서무관적인 성질이 불가피하게 적용되므로, 시간적 정보손실이 불가피하다. *
→ 시계열 모델링에서는 연속적인 시간적 관계가 위치관련한 것보다 중요하므로
4. An Embarrassingly Simple Baseline for LTSF
DMS 사용할 것
(기존 Transformer based LTSF문제들의 해결방안들 : 전부 IMS 사용(오류누적심함)
→ 이 연구에서는 DMS사용할것DMS기반 LTSF-Linear사용할 것
→ 과거값(L)을 입력으로 사용하고, T시점에서 한 번에 전체 예측을 수행
→ 모델이 각 변수의 중요도를 동일하게 고려하고, 변수 간에 공간적인 상관관계를 반영XDLinear와 NLinear 개념
DLinear: 시계열 데이터의 구성 요소를 분해하고 선형 레이어를 통해 각 구성 요소를 처리하는 방법**
NLinear: 데이터셋 분포 변화 클때 사용**
5. Experiments
Experimental Settings
- 사전 세팅 : 9개의 현실 데이터셋
특징 → 모두 다변량 시계열
→ MSE, MAE로 비교
→ 4개의 최신 Transformer based methods(FEDformer, Autoformer ,Informer ,Pyraformer ) 포함
→ naive DMS method: Closest Repeat : look-back 윈도우를 통해 이전의 데이터를 살펴보고, 윈도우 내의 마지막 값(가장 최근 값)을 반복하여 예측에 사용합니다. 예를 들어, 10개의 이전 데이터로 구성된 look-back 윈도우가 있다고 가정해봅시다. 해당 윈도우 내의 마지막 값이 50이라면, Repeat 방법은 이후의 예측에 계속해서 50을 사용)
Comparison with Transformers
Quantitative results
- 성능 측면
- 다변량 : 변수간 상관관계 없더라도 대부분 transformer적용보다 LTSF-Linear적용한게 예측 성능 좋음
- NLinear, DLinear : 분포 이동 및 trend-seasonality특징 처리하는데 좋음
- 일변량 : transformer적용보다 LTSF-Linear적용한게 예측 성능 좋음
- 다변량 : 변수간 상관관계 없더라도 대부분 transformer적용보다 LTSF-Linear적용한게 예측 성능 좋음
- Repeat method
- Exchange-Rate 데이터에서 성능이 젤 좋음 : Transformer based방법들은 일부 잡음에 대해 train data에서 과적합되어 정확도 감소
Qualitative results
- Transformer의 한계
- Transformer는 비주기적이고, 다른 시간적 패턴을 가진 데이터는 추세 및 결과를 예측 잘 못함
6. More Analyses on Transformer-Based Solutions
1) Can existing LTSF-Transformers extract temporal relations well from longer input sequences?
- 일반적으로 시계열 모델에서 LTSF-Linear 성능은 input look-back window size가 증가함에 따라 성능 향상
- Transformer는 look-back window size가 증가함에 따라 성능이 저하 or 안정적일수도
- 대부분의 Transformer들에는 input=96이 젤 적당함
2) What can be learned for long-term forecasting?
- Transformer는 단기 시계열 예측에만 유용
→ look-back window가 작아야 유용함! - 단기시계열
- look-back window 영향 큼
- 장기시계열
- look-back window 영향 작음
3) Are the self-attention scheme effective for LTSF?
- 결론
- self-attention같은 복잡한 디자인은 LTSF에 쓸모없다
- 확인 과정 (ex. Informer)
- 기존의 Transformer (예: Informer)에서 이러한 복잡한 디자인이 필수적인지 여부를 확인
- Informer를 점진적으로 Linear로 변환
- 1) Att.-Linear: 각 self-attention 레이어를 linear 레이어로 대체
- self-attention 레이어는 가중치가 동적으로 변하는 fully-connected 레이어로 간주
- 2) Embed + Linear: Informer의 다른 보조 디자인 (예: FFN)을 제거하여 임베딩 레이어와 linear 레이어만 남김
- 3) 모델을 단일 linear 레이어로 단순화
- 1) Att.-Linear: 각 self-attention 레이어를 linear 레이어로 대체
4) Can existing LTSF-Transformers preserve temporal order well?
- 결론
- 기존 LTSF-Transformer : 시간적 관계 제한적으로 보존,
- 모든 경우에 대해 LTSF-Linear의 성능 하락폭이 Transformer 기반 방법보다 크며, 이는 기존의 Transformer들이 시간적 순서를 잘 보존하지 못한다
5) How effective are different embedding strategies?
- Transformer들 위치, 시간 임베딩 유무 성능 비교
6) Is training data size a limiting factor for existing LTSF Transformers?
Transformer모델을 시간을 원래꺼와 줄였을때의 성능 비교
(Traffc 데이터셋에서 실험을 수행하여 전체 데이터셋 (17,544 * 0.7 시간)에서 훈련된 모델(Ori.)과 축소된 데이터셋 (8,760 시간, 즉, 1년)에서 훈련된 모델(Short)의 성능을 비교)
- 결과: 축소된 훈련 데이터를 사용한 예측 오차가 보통적으로 더 낮음
- 더 적은 데이터를 사용해야 한다는 결론을 내릴 수는 없지만, 이는 훈련 데이터의 규모가 제한적인 요인이 아니라는 것을 보여줌
7) Is effciency really a top-level priority?
- DMS 디코더를 사용하는 기본 Transformer와 비교했을 때, 대부분의 Transformer 변형은 실제로는 비슷하거나 더 나쁜 추론 시간과 매개변수를 유발
7. Conclusion and Future Work
Conclusion
- 장기 시계열 예측 문제에 대한 신흥 Transformer 기반 솔루션의 효과성을 의심합니다.
- 저희는 DMS 예측 기준선으로서 극히 간단한 선형 모델인 LTSF-Linear을 사용하여 주장을 검증
📖 사전 지식 자료
Transformer
1) 개념
트랜스포머(Transformer)는 2017년에 발표된 딥러닝 모델로, 주로 자연어 처리(Natural Language Processing, NLP) 작업에 사용되는 강력하고 혁신적인 아키텍처입니다. 이 모델은 기존의 순환 신경망(RNN) 기반 모델의 한계를 극복하고, 특히 긴 시퀀스 데이터를 처리하는데 뛰어난 성능을 발휘하여 자연어 처리 분야에서 혁신적인 발전을 이끌어냈습니다.
트랜스포머는 "Attention is All You Need"라는 논문에서 처음 소개되었으며, 구글 브레인(TensorFlow) 팀에 의해 개발되었습니다. 이 모델은 인코더와 디코더라는 두 가지 주요 구성 요소로 구성되어 있으며, 각각은 다수의 층으로 구성됩니다. 트랜스포머의 주요 특징은 다음과 같습니다:
- 어텐션(Attention) 메커니즘: 기존의 RNN과 LSTM과 같은 순환 신경망은 시퀀스 데이터를 순차적으로 처리하며 정보를 전달하는 방식이었습니다. 하지만 트랜스포머는 어텐션 메커니즘을 통해 입력 시퀀스의 모든 단어들을 동시에 처리하고, 특정 단어가 다른 단어들과 얼마나 연관되어 있는지를 계산합니다. 이를 통해 시퀀스 간의 관계를 더 잘 이해하고 처리할 수 있게 되었습니다.
- 셀프 어텐션(Self-Attention): 트랜스포머의 인코더와 디코더 층은 셀프 어텐션 메커니즘을 사용합니다. 이는 입력 시퀀스 내의 각 단어가 서로 어떻게 관련되어 있는지를 계산하여 가중치를 부여하는 방식입니다. 이를 통해 모델은 문장 내의 단어들 사이의 문맥을 파악하고 중요한 정보를 잘 추출할 수 있습니다.
- 위치 인코딩(Positional Encoding): 트랜스포머는 입력된 단어들의 위치 정보를 학습하는 데에 순서 정보가 없는 멀티헤드 어텐션을 사용합니다. 따라서 위치 정보를 주입하여 각 단어의 상대적인 위치를 모델에게 알려주어야 합니다. 이를 위해 위치 인코딩을 사용하여 단어의 상대적인 위치 정보를 임베딩에 추가합니다.
- 멀티헤드 어텐션(Multi-Head Attention): 트랜스포머에서는 어텐션을 여러 개의 헤드로 분할하여 독립적으로 계산하는 멀티헤드 어텐션을 사용합니다. 이를 통해 다양한 관점에서의 어텐션 정보를 학습하고, 모델의 성능을 향상시킵니다.
트랜스포머는 기존의 NLP 작업들을 획기적으로 개선시키면서, 특히 번역과 같은 시퀀스-투-시퀀스(Seq2Seq) 작업에 매우 성공적으로 적용되었습니다. 이후 많은 변형 모델들이 개발되어 다양한 자연어 처리 작업에 응용되고 있으며, 트랜스포머 아키텍처는 자연어 처리 분야의 핵심 기술로 자리잡고 있습니다.
2) transformer에서 self-attention으로 인해 정보손실 어떻게?
시계열 데이터가 [10, 20, 30, 40]이라고 가정.
- Transformer 모델은 이 데이터를 (토큰으로 분할하고 임베딩을 적용)한 뒤 self-attention을 통해 처리.
그러나 self-attention은 순서 정보를 고려하지 않고 각 토큰을 독립적으로 처리하기 때문에,
[10, 20, 30, 40]과 [30, 20, 40, 10]을 동일하게 취급.
이는 일부 상대적인 순서 정보는 보존되지만, 절대적인 시간적인 흐름에 대한 정보는 손실될 수 있다는 의미
3) Transformer에서 self-attention의 역할 및 효과?
- Long-range 의존성 학습: 모든 위치가 다른 위치와 상호작용하기 때문에, 장기적인 의존성을 더 쉽게 학습
- 효율적인 정보 전달: 입력의 중요한 부분에 집중하여 효율적인 정보 전달
4) 희소성 편향? low rank property?
- 희소성 편향
Sparsity bias(희소성 편향)란, 특정 데이터 또는 정보가 다른 데이터에 비해 상대적으로 희소하게 분포되어 있을 때 발생하는 경향을 가리키는 용어. .
이때, 중요한 정보가 희소하게 분포되어 있다면, 모델은 그 중요한 정보에 더 집중하고 학습하도록
⇒ 입력 시퀀스를 분할해서 데이터를 희소하게 만들어서, 중요 정보에 더 집중하도록 - low rank property
self-attention은 입력 시퀀스의 길이에 따라 큰 행렬 연산을 수행해야 합니다. 이러한 연산은 계산량이 많고 메모리 사용량도 증가시키는 단점이 있습니다. 하지만 일부 행렬은 실제로는 다른 행렬로 근사될 수 있는 경우가 있습니다. 이렇게 근사 가능한 행렬을 저차원의 행렬로 대체하는 것을 저차원 속성
⇒ 입력시퀀스의 행렬을 저차원 행렬로 줄여서, 중요 정보에 더 집중하도록- 저차원 근사: self-attention 레이어에서 사용되는 일부 행렬을 더 낮은 차원의 행렬로 근사
- 저차원 연산: self-attention 계산을 수행할 때 행렬 연산을 저차원의 연산으로 대체
5) 변형들
LogTrans
개념
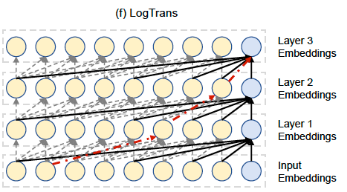
희소성 편향이 어케 적용?
LogTrans에서는 이러한 계산 복잡도를 줄이기 위해 입력 시퀀스를 여러 세그먼트로 분할합니다. 그리고 각 세그먼트에 대해 self-attention을 적용할 때, 이전 세그먼트와의 관계를 고려하여 연결되는 부분만을 선택합니다. 이렇게 함으로써 특정 세그먼트와 연결된 부분만을 집중적으로 계산하고, 다른 부분은 무시함으로써 계산량을 크게 줄입니다.
이 과정은 마치 공을 미로 속으로 놓고 특정 규칙에 따라 미로를 통과시키는 것과 비슷합니다. 희소성 편향은 마치 어떤 통로를 통해 통과시킬지를 선택하는 규칙이라고 생각할 수 있습니다. 이렇게 선택된 통로만을 따라 self-attention 연산을 수행하여 계산 비용을 줄임
- Transformer 모델을 기반으로 한 로그 데이터 분석을 위한 변형 모델
- 로그 데이터는 주로 시계열 형태로 구성
- self-attention과 시계열 특성을 고려하여 로그 데이터의 패턴을 학습하고 예측
- Encoder
- LogSparse , convolutional self-attention
- Decoder
- IMS(Iterated Multi-Step)
Informer
개념
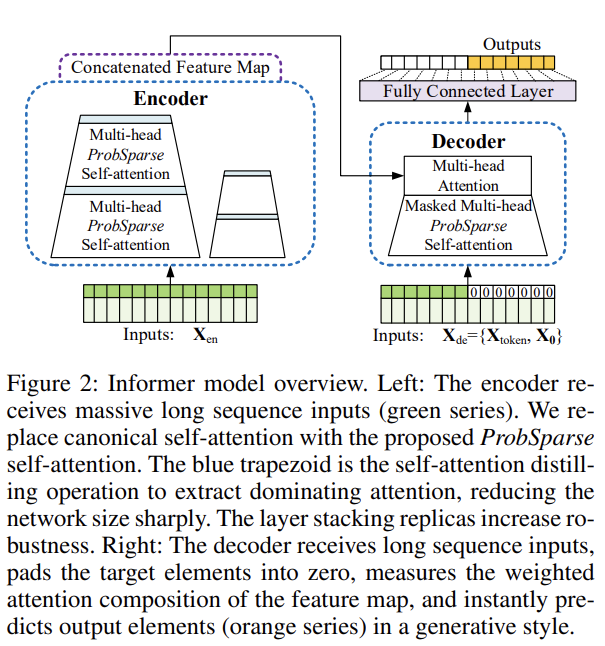
- 시계열 데이터에 대한 예측을 수행하는 Transformer 기반의 모델
- 입력 시퀀스의 길이와 패턴을 고려하여 자동으로 가변적인 길이의 시계열 데이터를 처리
- Encoder
- ProbSparse and distiliting self-attention
- Decoder
- DMS(Direct Multi-Step)
Autoformer
개념
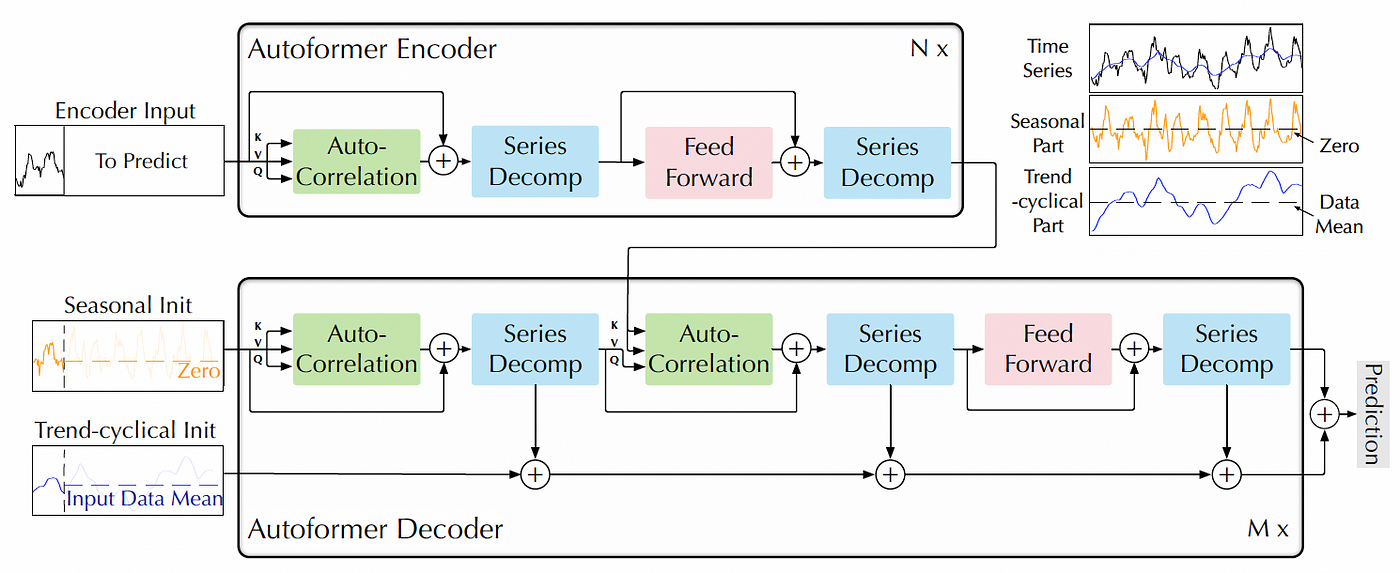
- 자동 기계 학습 모델 구조 탐색(automated model architecture search)을 위한 Transformer 기반의 모델
- 네트워크 구조, 층 수, 헤드 수, 임베딩 차원 등의 하이퍼파라미터를 자동으로 조정
- series auto correlation with decomposition (서로 다른 시간 간격만큼 데이터가 얼마나 상관되어 있는지) : 자기상관성은 주기성과 추세 등의 패턴을 파악하는 데 도움이 되며, 시계열 데이터의 미래 값을 예측하거나 시계열 모델을 구축하는 데 중요한 정보를 제공
- Encoder
- Series auto-correlation with decomposition
- Decoder
- DMS with auto-correlation and decomposition
Pyraformer
개념
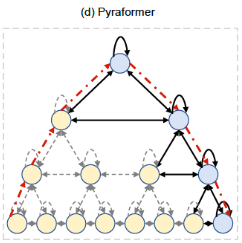
희소성 편향이 어케 적용?
- 입력 시퀀스를 여러 레벨의 피라미드 구조로 분할하고, 각 레벨에서 self-attention을 수행하는 방식
피라미드 구조(pyramid structure)를 활용하여 입력 시퀀스의 길이에 따라 유연하게 처리할 수 있는 Transformer 기반의 모델
입력 시퀀스를 여러 다양한 해상도로 다운샘플링하고, 각 해상도에서의 정보를 합성하여 전체 시퀀스에 대한 표현을 생성
- Encoder
- Multi-resolution pyramid attention
- Decoder
- DMS along spatio-temporal dimension
FEDformer
개념
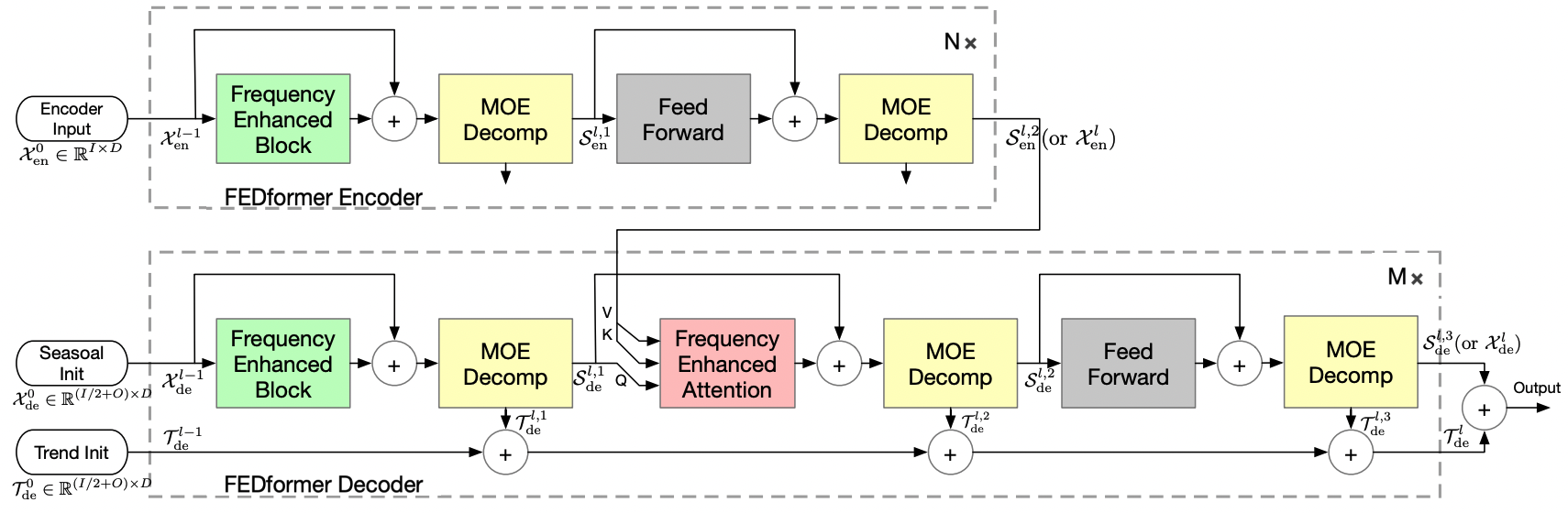
- 데이터 분산 학습을 위한 효율적인 Transformer 기반 모델
- Federated Learning + Transformer
- 여러 개의 클라이언트에서 분산된 데이터를 학습하고 전역 모델을 업데이트
- 중앙 집중화된 데이터를 전송하지 않고, 로컬 데이터에서 그래디언트를 계산하여 개인 정보 보호와 데이터 보안을 강화
- Encoder
- Frequency enhanced block with decomposition
- Decoder
- DMS with frequency attention and decomposition
Repeat
개념

Seasonal-Trend Decomposition

연간 매출 데이터를 가정해보면, 계절적 패턴(예: 연말에 매출이 증가하는 경향)과 전반적인 추세(예: 연간 매출이 점차 상승하는 경향)
장점
시계열 데이터는 시간에 따라 변화하는 데이터이기 때문에, 계절성과 추세를 분해하여 개별 구성 요소를 분석함으로써 데이터의 특성을 파악할 수 있습니다. 이를 통해 다음과 같은 이점을 얻을 수 있습니다:
- 계절성 추정: 계절성-추세 분해를 통해 계절성 구성 요소를 추정할 수 있습니다. 이를 통해 데이터의 주기적인 변동성을 확인하고, 계절성 패턴을 파악할 수 있습니다. 예를 들어, 매월 판매량 데이터에서 계절성 구성 요소를 추정하여 매년 같은 시기에 어떤 제품이 가장 많이 팔리는지를 확인할 수 있습니다.
- 추세 파악: 추세 구성 요소를 추정함으로써 데이터의 장기적인 변동성을 파악할 수 있습니다. 추세는 데이터가 장기적으로 증가하거나 감소하는 경향을 보여줍니다. 이를 통해 시장 동향을 예측하거나 장기적인 패턴을 파악할 수 있습니다.
- 잔차 분석: 잔차는 계절성과 추세를 제외한 나머지 변동성을 나타냅니다. 잔차를 분석함으로써 계절성과 추세로 설명되지 않는 불규칙한 요소들을 파악할 수 있습니다. 이를 통해 예측 모델의 정확도를 높이거나, 데이터의 이상치를 감지할 수 있습니다.
Etc
Naive DMS, DMS, IMS
개념
- Naive DMS
- 다음 시간 단계의 값을 예측하기 위해 이전 시간 단계의 값을 사용
- DMS
- 여러 시간 단계를 한 번에 예측하는 방법
- 이전 시간 단계의 값을 사용하여 한 번에 다음 여러 시간 단계를 예측
- IMS
- 예측된 값을 다시 입력으로 사용하여 반복적으로 예측하는 방법
- Naive DMS
예시
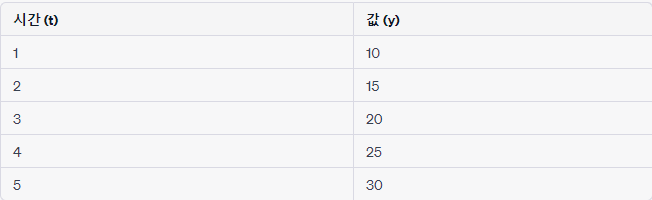
Naive DMS
- t=6의 값을 예측하려면, t=5의 값을 그대로 사용.
예측: t=6, y=30
- t=6의 값을 예측하려면, t=5의 값을 그대로 사용.
DMS
- t=6, t=7, t=8의 값을 예측하려면, 이전 시간 단계의 값을 사용하여 한 번에 세 가지 값을 예측
예측: t=6, y=35 t=7, y=40 t=8, y=45
- t=6, t=7, t=8의 값을 예측하려면, 이전 시간 단계의 값을 사용하여 한 번에 세 가지 값을 예측
IMS
- t=6, t=7, t=8의 값을 예측하려면, 이전 시간 단계의 값을 사용하여 첫 번째 예측을 수행하고, 이 예측값을 다시 입력으로 사용하여 두 번째 예측을 수행. 이러한 과정을 반복하여 여러 시간 단계를 예측
예측: t=6, y=35 (t=5의 값 사용) t=7, y=40 (t=6의 예측값 사용) t=8, y=45 (t=7의 예측값 사용)
- t=6, t=7, t=8의 값을 예측하려면, 이전 시간 단계의 값을 사용하여 첫 번째 예측을 수행하고, 이 예측값을 다시 입력으로 사용하여 두 번째 예측을 수행. 이러한 과정을 반복하여 여러 시간 단계를 예측