[논문 리뷰] Towards Explaining Distribution Shifts (ICML 2023)

방법론의 목적
기존 연구 대부분은 변화가 발생했는지 여부를 탐지하는 데에만 초점을 맞추고 있으며, 탐지된 변화를 인간이 적절히 이해하고 처리할 수 있다고 가정함.
이러한 수작업 완화 작업을 지원하기 위해, 원본 분포에서 변환된 분포로 이동을 설명할 수 있도록 함.
class distribution shift에 대한 대응 (=ex. 이상일때 shift발생하는데, 정상일때와 뭐가 다르길래 발생하는지 알려줌)
 
 
주목해야할 점
Interpretable Transportation Map을 활용하여 분포 변화를 설명하는 방법론

• Transportation Map
  • 소스와 타겟 두 분포 사이의 관계를 설명하기 위해, 데이터를 한 분포에서 다른 분포로 변환하는 map
  • ex. 변환 맵이 간단한 수학 공식이나 명확한 규칙으로 표현된다면, 이를 사용해 어떤 변화가 발생했는지 쉽게 설명

⇒ 최종 목표: 이해하기 쉬운 방식으로 소스와 타겟 분포를 연결하는 방법을 찾는 것
 
 
방법론

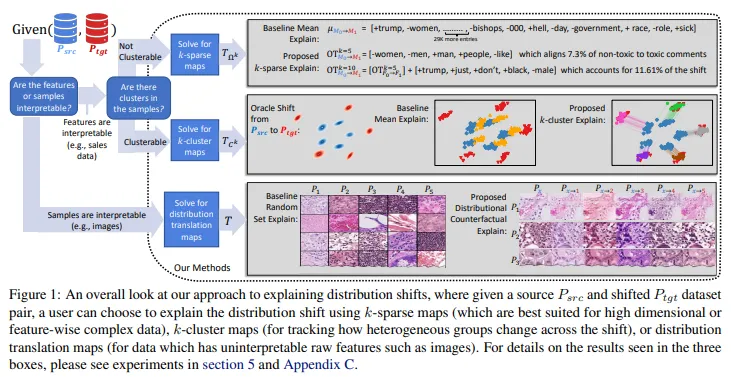
• K-sparse Transport
  • 목적: 고차원 데이터에서 일부 차원에서만 분포 이동이 발생할 때, 이를 해석 가능한 방식으로 설명하는 것을 목표로 함.
  • ex. 다차원 센서 네트워크에서 특정 센서들만 환경 변화에 반응하는 경우 유용
  • 방법: 최적 수송(Optimal Transport, OT)을 기반으로 하고, 다음과 같은 제약을 추가하여 해석 가능한 맵을 생성
    • 각 샘플의 이동이 최대 k개의 차원에만 영향을 미치도록 제한.
    • 수식으로는, 활성 차원 집합 A(T)를 정의하여, T가 이동시키는 차원의 개수를 k 이하로 제한

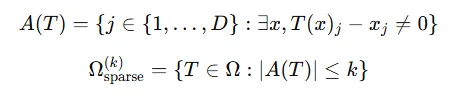
• • 구체적 알고리즘:
    1. 평균 차이 계산:
       • 소스 데이터(X)의 각 차원별 평균과 타겟 데이터(Y)의 각 차원별 평균을 비교.
       • 평균 차이가 큰 순서대로 특징(차원)을 정렬.
    2. 중요한 차원 선택:
       • 평균 차이가 큰 상위 k개의 차원을 선택.
       • 나머지 차원은 고정.
    3. 선택된 차원만 이동:
       • 선택된 차원의 값만 조정하여, 소스 데이터가 타겟 데이터와 더 비슷하게 만듦.
       • 조정 방식:

       • 

    4. Wasserstein 거리 계산:
       • 이동 후 전체 분포가 얼마나 가까워졌는지 측정.
    1.  
  • 효과
    • 고차원 데이터에서 이동의 주요 차원을 강조하여, 사용자가 특정 차원에 대한 이해를 쉽게 할 수 있음.
    • 단순한 평균 이동(mean shift) 방식보다 더 세밀한 이동 설명 제공.

 
 

• K-Cluster Transport
  • 목적 : k-Cluster Transport는 분포 이동이 데이터 내의 이질적 하위 그룹들에 따라 달라질 때, 이를 효과적으로 추적하고 설명하는 것을 목표로 함.
  • 방법: 데이터 분포를 k개의 하위 집단으로 나누고, 각 집단별 이동 벡터를 계산
    • 클러스터 기반 이동 맵:

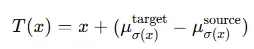
여기서 σ(x)는 클러스터 레이블을 반환하는 함수

• 알고리즘
  1. 최적 수송 맵(TOT)을 계산하여, 소스와 타겟 데이터를 페어링.
  2. k-평균(K-Means)을 사용하여 클러스터 생성.
  3. 각 클러스터에 대한 평균 이동 벡터 계산.
• 효과
  • 그룹 간 이동의 세부적인 차이를 드러내어, 특정 하위 집단에 초점을 맞춘 정책 설계가 가능.
  • 평균 이동 방식이나 단순 피처 중요도 분석보다 구체적인 통찰 제공.

 
이 방법론 장점

• k-Sparse Transport
  • 해석 가능성(Interpretability):
    • 데이터의 이동이 제한된 k개의 중요한 차원(특징)에 집중되므로, 분포 이동의 원인을 명확히 설명할 수 있습니다.
    • 예: 고차원 데이터에서 "어떤 특정 변수"가 이동에 가장 큰 영향을 미쳤는지 파악 가능.
  • 효율성(Efficiency)
    • 제한된 k개의 차원만 고려하므로 계산 비용이 상대적으로 낮음.
    • 고차원 데이터에서 전체 차원을 다루는 것보다 간결한 분석 가능.
  • 잡음 감소(Noise Reduction):
    • 중요하지 않은 차원에서의 이동은 배제하므로, 분포 이동의 신뢰성을 높임.
  • 설명력 강조:
    • 이동 설명 비율(PercentExplained)을 통해 이동의 주요 원인을 정량화.

• k-Cluster Transport
  • 하위 집단(Subgroup) 수준에서의 분석:
    • 데이터를 k개의 클러스터로 나누고, 클러스터별로 이동을 계산하므로, 하위 집단 간의 차이를 분석할 수 있습니다.
    • 예: 특정 연령대나 소득 그룹에서의 이동 양상을 개별적으로 이해.
  • 복잡한 데이터의 구조적 이동 설명:
    • 단일 차원에서 설명하기 어려운 데이터 이동을, 클러스터라는 구조적 단위로 분석 가능.
    • 예: 비선형적 이동이나 복잡한 상호작용 효과를 파악.
  • 유연성(Flexibility):
    • 클러스터 개수(k)를 조정하여 분석 수준을 사용자 정의할 수 있음:
      • k = 1: 단순 이동 분석.
      • k>1: 세밀한 하위 집단 분석.
  • 데이터 그룹 간 관계를 명확히:
    • 단순히 소스와 타겟 전체 분포를 비교하는 대신, 데이터 그룹 내 다양한 패턴을 고려